
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
先化简后求值 2(x2y+xy2)﹣2(x2y﹣3x)﹣2xy2﹣2y的值,其中x=﹣1,y=2.
6x﹣2y,﹣10 【解析】试题分析:本题考查了整式的化简求值,整式的化简就是去括号合并同类项,去括号时一是不要漏乘括号内的项,二是括号前是“-”时,去掉括号后括号内的各项都要变号. 2(x2y+xy2)﹣2(x2y﹣3x)﹣2xy2﹣2y =2x2y+2xy2﹣2x2y+6x﹣2xy2﹣2y =6x﹣2y, 当x=﹣1,y=2时, 原式=6x﹣2y=6×(-1...查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
解方程:
(1)1﹣3(x﹣2)=4; (2)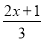 ﹣
﹣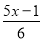 =1.
=1.
查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
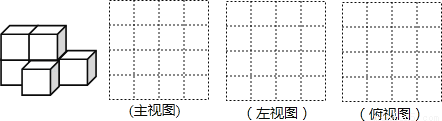
如图,由六个棱长为1cm的小正方体组成一个几何体.
(1)分别画出这个几何体的主视图、左视图、俯视图.
(2)该几何体的表面积是__cm2.
查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
已知∠1与∠2互为补角,且∠1比∠2大20°,求∠1、∠2的度数.
100°. 【解析】试题分析:本题考查了补角的定义,设∠2=x,则∠1=x+20,根据∠1与∠2互为补角,即 ∠1+∠2=180列方程求解. 【解析】 设∠2=x,则∠1=x+20, 由题意得:∠1+∠2=x+20+x=180, ∴x=80°, ∴∠2=80°,∠1=x+20°=100°.查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
如图,C是线段AB的中点.
(1)若点D在CB上,且DB=2cm,AD=8cm,求线段CD的长度;
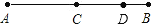
(2)若将(1)中的“点D在CB上”改为“点D在CB的延长线上”,其它条件不变,请画出相应的示意图,并求出此时线段CD的长度.
(1)3cm;(2)5cm. 【解析】试题分析:(1)根据线段的和,可得AB的长,根据线段中点的性质,可得BC的长,再根据线段的差,可得答案. (2)根据题意画出图形,利用线段的差,可得AB的长,根据线段中点的性质,可得BC的长,再根据线段的和,可得答案. 【解析】 (1)由线段的和差,得AB=AD+DB=8+2=10cm, 由C是AB的中点,得BC=AB=5cm, ...查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
元旦来临前,七年级(1)班课外活动小组计划做一批“中国结”.如果每人做6个,那么比计划多了7个;如果每人做5个,那么比计划少了13个.该小组计划做多少个“中国结”?
113. 【解析】 试题分析:设小组成员共有x名,由题意可知计划做的中国结个数为:(6x-7)或(5x+13)个,令二者相等,即可求得x的值,可得小组成员个数及计划做的中国结个数. 试题解析:设小组成员共有x名,则计划做的中国结个数为:(6x-7)或(5x+13)个 ∴6x-7=5x+13 解得:x=20, ∴6x-7=113, 答:计划做113个中国结....查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
旅行社组织了甲、乙两个旅游团到游乐场游玩,两团总报名人数为120人,其中甲团人数不超过50人,游乐场规定一次性购票50人以上可享受团队票.门票价格如下:
门票类别 | 散客票 | 团队票A | 团队票B |
购票要求 | 超过50人但不超过100人 | 超过100人 | |
票价(元/人) | 80元/人 | 70元/人 | 60元/人 |
旅行社经过计算后发现,如果甲、乙两团合并成一个团队购票可以比分开购票节约300元.
(1)求甲、乙两团的报名人数;
(2)当天到达游乐场后发现团队票价格作了临时调整,团队票A每张降价a元,团队票B每张降价2a元,同时乙团队因故缺席了30人,此时甲、乙两团合并成一个团队购票可以比分开购票节约225元,求a的值.
(1)甲团15人,乙团105人;(2)a=5. 【解析】试题分析:(1)根据甲团队人数为x人,乙团队人数不超过50人,得到x≥70,分两种情况:①当70≤x≤100时,分开购票-甲、乙两团合并成一个团队购票=300元,②当x>100时,分开购票-甲、乙两团合并成一个团队购票=300元,分别列出方程,即可解答; (2)根据每张门票降价a元,利用甲、乙两团合并成一个团队购票可以比分开购票节...查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
如图,直线l上有A、B两点,AB=12cm,点O是线段AB上的一点,OA=2OB.
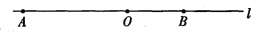
(1)OA= cm,OB= cm;
(2)若点C是线段AB上一点,且满足AC=CO+CB,求CO的长;
(3)若动点P、Q分别从A、B同时出发,向右运动,点P的速度为2cm/s,点Q的速度为1cm/s,设运动时间为ts.当点P与点Q重合时,P、Q两点停止运动.
①当t为何值时,2OP-OQ=4;
②当点P经过点O时,动点M从点O出发,以3cm/s的速度也向右运动.当点M追上点Q后立即返回,以3cm/s的速度向点P运动,遇到点P后再立即返回,以3cm/s的速度向点Q运动,如此往返,直到点P、Q停止时,点M也停止运动.在此过程中,点M行驶的总路程是多少?
(1)OA=8cm,OB=4cm;(2);(3)① 当P在点O左侧时,;当P在点O右侧时,t=8;② 24cm 【解析】 试题分析:(1)由于AB=12cm,点O是线段AB上的一点,OA=2OB,则OA+OB=3OB=AB=12cm,依此即可求解;(2)根据图形可知,点C是线段AO上的一点,可设CO的长是xcm,根据AC=CO+CB,列出方程求解即可;(3)①分0≤t<4;4≤t<6;...查看答案和解析>>
科目: 来源:江苏省盐城市2017-2018学年七年级12月月考数学试卷 题型:解答题
探究实验:《钟面上的数字》
实验目的:了解钟面上时针与分针在转动时的内在联系,学会用一元一次方程解决钟面上的有关数学问题,体会数学建模思想.
实验准备:机械钟(手表)一只
实验内容与步骤:
观察与思考:
(1)时针每分钟转动__°,分针每分钟转动__°.
(2)若时间为8:30,则钟面角为__°,(钟面角是时针与分针所成的角)
操作与探究:
(1)转动钟面上的时针与分针,使时针与分针重合在12点处.再次转动钟面上的时针与分针,算一算,什么时刻时针与分针再次重合?一天24小时中,时针与分针重合多少次?(一天中起始时刻和结束时刻时針与分针重合次数只算一次,下同)
(2)转动钟面上的时针与分针,使时针与分针重合在12点处,再次转动钟面上的时针与分针,算一算,什么时刻钟面角第一次为90°?一天24小时中,钟面角为90°多少次?
拓展延伸:
一天24小时中,钟面角为180°__次,钟面角为n°(0<n<180)____次.(直接写出结果)

查看答案和解析>>
科目: 来源:黑龙江省哈尔滨市双城区2017-2018学年八年级上学期期末考试数学试卷 题型:单选题
下列运算中,正确的是( )
A. 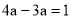 B.
B. 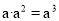 C.
C. 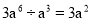 D.
D. 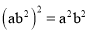
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com