
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:填空题
矩形纸片ABCD中,已知AD=8,AB=6,E是边BC上的点,以AE为折痕折叠纸片,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为 .
3或6 【解析】试题分析: 由题意可知有两种情况,见图1与图2; 图1:当点F在对角线AC上时,∠EFC=90°, ∵∠AFE=∠B=90°,∠EFC=90°, ∴点A、F、C共线, ∵矩形ABCD的边AD=8, ∴BC=AD=8, 在Rt△ABC中,AC==10, 设BE=x,则CE=BC﹣BE=8﹣x, 由翻折的性质得,AF=AB=6...查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:填空题
如图,矩形ABCD的周长为20cm,两条对角线相交于O点,过点O作AC的垂线EF,分别交AD、BC于E、F点,连结CE,则△CDE的周长为 cm.
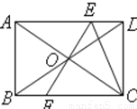
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
解方程: 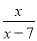 -
-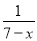 =2.
=2.
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
已知:如图,在平行四边形ABCD中,E、F是对角线AC上的两点,且AE=CF.求证:∠EBF=∠EDF.
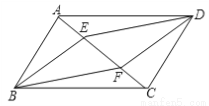
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
(本题8分)射击队为从甲、乙两名运动员中选拔一人参加比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 平均成绩 | 中位数 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 | 9 | ① |
乙 | 10 | 7 | 10 | 10 | 9 | 8 | ② | 9.5 |
(1)完成表中填空① ;② ;
(2)请计算甲六次测试成绩的方差;
(3)若乙六次测试成绩方差为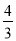 ,你认为推荐谁参加比赛更合适,请说明理由.
,你认为推荐谁参加比赛更合适,请说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
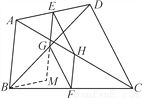
在四边形ABCD中,E、F分别是AD、BC的中点,G、H分别是BD、AC的中点,当AB、CD满足什么条件时,四边形EGFH是菱形?请证明你的结论.(提示:过点B作BM∥AD交EG的延长线于点M,证明EG//AB且EG=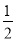 AB)
AB)
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
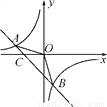
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b的图象和反比例函数y=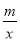 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)若D(x,0)是x轴上原点左侧的一点,且满足kx+b-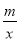 <0,求x的取值范围.
<0,求x的取值范围.
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
(10分)某单位准备印制一批证书,现有两个印刷厂可供选择,甲厂费用分为制版费和印刷费两部分先收取固定的制版费,再按印刷数量收取印刷费,乙厂直接按印刷数量收取印刷费.甲厂的总费用y1(干元)、乙厂的总费用y2(千元)与印制证书数量x(千个)的函数关系图分别如图中甲、乙所示.
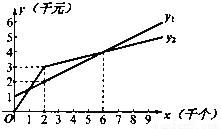
(l)甲厂的制版费为____千元,印刷费为平均每个 元,甲厂的费用yl与证书数量x之间的函数关系式为 ,
(2)当印制证书数量不超过2千个时,乙厂的印刷费为平均每个 元;
(3)当印制证书数量超过2干个时,求乙厂的总费用y2与证书数量x之间的函数关系[式;
(4)若该单位需印制证书数量为8干个,该单位应选择哪个厂更节省费用?请说明理由.
(1)1;0.5;y=0.5x+1; (2)1.5; (3); (4)由图象可知,当x=8时,y1>y2,因此该单位选择乙厂更节省费用. 【解析】 试题分析:(1)由图得制版费是1千元,通过坐标(0,1)(2,2)求出函数解析式,印刷单价=(印刷费用-制版费)÷2000; (2)由图像可知,用3千元÷2千个,即可得到乙厂的平均印刷费; (3)设y2=kx+...查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:解答题
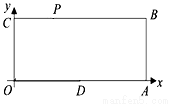
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动。
(1) 求梯形ODPC的面积S与时间t的函数关系式。
(2) t为何值时,四边形PODB是平行四边形?
(3) 在线段PB上是否存在一点Q,使得ODQP为菱形。若存在求t值,若不存在,说明理由。
(4) 当△OPD为等腰三角形时,求点P的坐标。
查看答案和解析>>
科目: 来源:2017-2018学年八年级数学下册(华师大版):期末检测1 题型:填空题
探究证明:
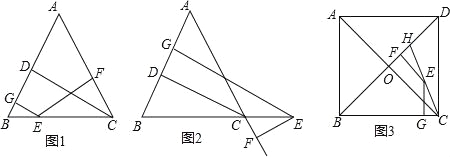
(1)如图1,在△ABC中,AB=AC,点E是BC上的一个动点,EG⊥AB,EF⊥AC,CD⊥AB,点G,F,D分别是垂足.求证:CD=EG+EF;
猜想探究:
(2)如图2,在△ABC中,AB=AC,点E是BC的延长线上的一个动点,EG⊥AB于G,EF⊥AC交AC延长线于F,CD⊥AB于D,直接猜想CD、EG、EF之间的关系为 CD=EG﹣EF ;
问题解决:
(3)如图3,边长为10的正方形ABCD的对角线相交于点O、H在BD上,且BH=BC,连接CH,点E是CH上一点,EF⊥BD于点F,EG⊥BC于点G,则EF+EG= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com