
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:单选题
将一条长30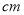 的铁丝剪成两段,并把每一段铁丝做成一个正方形,要使这两个正方形的面积之和等于86
的铁丝剪成两段,并把每一段铁丝做成一个正方形,要使这两个正方形的面积之和等于86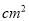 ,现设其中一个正方形的周长为
,现设其中一个正方形的周长为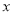 ,根据题意可列方程为( )
,根据题意可列方程为( )
A. 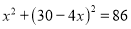 B.
B. 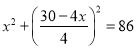
C. 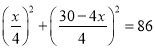 D.
D. 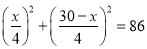
查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:单选题
某市防洪大堤的横截面如图所示,已知AE∥BC,背水坡AB的坡度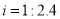 ,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
,且AB=26米.身高1.8米的小明竖直站立于A点,眼睛在M点处测得竖立的高压电线杆顶端D点的仰角为24°,已知地面CB宽30米,则高压电线杆CD的高度约为( )(结果精确到整数,参考数据:sin24°≈0.40,cos24°≈0.91,tan24°≈0.45)
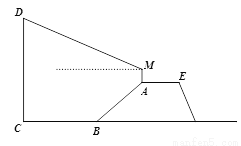
A. 33米 B. 34米 C. 35米 D. 36米
D 【解析】试题分析:过A点作AF垂直于CB的延长线于点F. ∵i=1:2.4,AB=26米, ∴AF:BF=1:2.4, 设AF=x米,则BF=2.4x米, 由勾股定理得:x2+(2.4x)2=262, 解得:x=10, 则AF=10米,BF=24米, ∴CN=FM=AF+AM=10+1.8=11.8, MN=CF=CB+BF=30+24=5...查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:单选题
在下列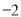 ,
, 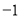 ,0,1,2,3这6个数中任取一个数记作
,0,1,2,3这6个数中任取一个数记作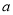 ,放回去,再从这六个数中任意取一个数记作
,放回去,再从这六个数中任意取一个数记作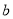 ,则使得分式方程
,则使得分式方程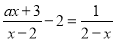 有整数解,且使得函数
有整数解,且使得函数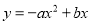 的图象经过第一三四象限的所有
的图象经过第一三四象限的所有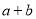 的值有( ).
的值有( ).
A. 2个 B. 4个 C. 5个 D. 8个
C 【解析】试题分析: -2=, 去分母得:ax+3-2x+4=-1, (a+2)x=-8, x=, 当a=-2时,x=2,分式方程无意义; 当a=0时,x=4; 当a=1时,x=8; 当a=3时,x=-8. 当a=0时,y=bx,是正比例函数,只经过两个象限,不符合题意; 当a=1时,y=-x2+bx,当对称轴x=>0时图象才经过一三四...查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:填空题
四条线段a、b、c、d成比例,其中b=3,c=2,d=6,那么a=____________.
1 【解析】试题分析:∵四条线段a、b、c、d成比例, ∴, ∵b=3,c=2,d=6, ∴, 解得:a=1. 故答案为:1.查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:填空题
计算: 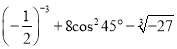 =____________.
=____________.
查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:填空题
某校举行春季运动会,需要在初二年级选取一名志愿者.初二(1)班、初二(2)班、初二(3)班各有2名同学报名参加.现从这6名同学中随机选取一名,则被选中的这名同学恰好来自初二(3)班的概率是___________.
【解析】试题分析:∵在这6名同学中,有2人来自初二(3)班, ∴被选中的这名同学恰好是初二(3)班同学的概率是=. 故答案为: .查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:填空题
关于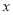 的一元二次方程
的一元二次方程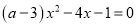 有实数根,则a满足_______________.
有实数根,则a满足_______________.
查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:填空题
如图,在平面直角坐标系中,菱形ABCD在第一象限内,AB=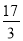 ,对角线BD与
,对角线BD与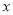 轴平行,B,C两点的横坐标分别为
轴平行,B,C两点的横坐标分别为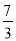 、5,反比例函数
、5,反比例函数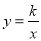 的图象经过B,C两点,则
的图象经过B,C两点,则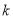 的值为___________.
的值为___________.
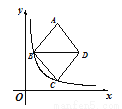
查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:填空题
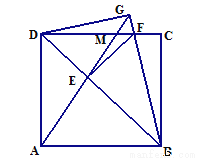
如图,已知在正方形ABCD中,F是CD边上一点(不与C、D重合),过点D作DG⊥BF交BF延长线于点G.连接AG,交BD于点E,交CD于点M,连接EF.若DG=4,AG=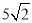 ,则EF的长为____________.
,则EF的长为____________.
查看答案和解析>>
科目: 来源:四川外语学院重庆第二外国语学校2018届九年级上学期第二次月考数学试卷 题型:解答题
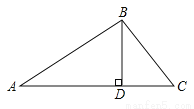
如图,在△ABC中,BD⊥AC,AB=8,AC=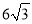 ,∠A=30°.
,∠A=30°.
(1)请求出线段AD的长度;
(2)请求出sin∠C的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com