数学课上老师提出了下面的问题：

在正方形ABCD对角线BD上取一点F，使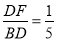.小明的做法如下：如图，

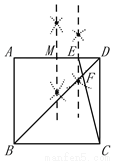
①应用尺规作图作出边AD的中点M;

②应用尺规作图作出MD的中点E;

连接EC，交BD于点F.

所以F点就是所求作的点.

请你判断小明的做法是否正确，并说明理由.

正确，理由见解析. 【解析】试题分析： 由作图易得，再证△DEF∽△BFC可得，由此即可得到，从而说明小明的做法正确. 试题解析： 小明的做法正确，理由如下： 由做法可知M为AD的中点，E为MD的中点， ∴， ∵四边形ABCD是正方形， ∴AD=BC，ED∥BC， ∴△DEF∽△BFC， ∴=， ∵AD=BC ∴==， ...

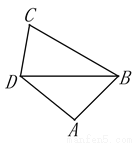
已知：如图，在四边形ABCD中，BD是一条对角线，∠DBC=30°，∠DBA=45°，∠C=70°.若DC=a，AB=b, 请写出求tan∠ADB的思路.（不用写出计算结果）

思路见解析. 【解析】试题分析： 过D点作DE⊥BC于点E，构造出Rt△CDE和Rt△DEB，由∠C=70°和DC=a可求出DE的长；由DE的长结合∠DBC=30°可求出BD的长；过点A作AF⊥BD于点F，构造出Rt△ADF和Rt△ABF；在Rt△ABF由∠ABD=45°，AB=b可求出BF和AF；由求出的BD和BF的长，可求出DF的长；最后在Rt△ADF中，由AF和DF的长即可求出t...

如图，在四边形ABCD中，AD∥BC，∠ADC=90°，点E是BC边上一动点，联结AE，过点E作AE的垂线交直线CD于点F.已知AD=4cm，CD=2cm，BC=5cm，设BE的长为x cm，CF的长为y cm.

小东根据学习函数的经验，对函数y随自变量x的变化而变化的规律进行探究.下面是小东的探究过程，请补充完整：

(1)通过取点、画图、测量，得到了x与y的几组值，如下表：

(说明：补全表格时相关数据保留一位小数)

(2)建立直角坐标系，描出以补全后的表中各对对应值为坐标的点，画出该函数的图象；

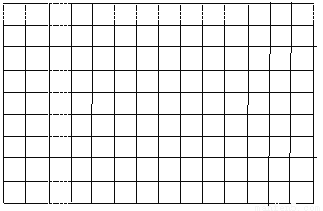
(3)结合画出的函数图象，解决问题: 当BE=CF时，BE的长度约为 cm.

（1）1.5；（2）画图见解析；（3）0.7(0.6~0.8均可以) 【解析】试题分析： （1）观察、分析表格中的数据可发现：x的取值从0到5是关于x=3对称出现的，对应的y的值的已知部分也是对应对称出现的，由此可推断x=4对应的y的值和x=2对应的y的值相等； （2）根据补全的表格中的数据，在坐标系中描点，再用平滑的曲线连接各点即可得到该函数的图象； （3）结合表格中的数...

在平面直角坐标系xOy中，直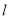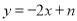线: 与抛物线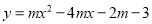相交于点A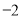（,7）.

(1)求m，n的值；

(2)过点A作AB∥x轴交抛物线于点B，设抛物线与x轴交于点C、D(点C在点D的左侧)，求△BCD的面积；

(3)点E（t,0）为x轴上一个动点，过点E作平行于y轴的直线与直线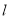和抛物线分别交于点P、Q.当点P在点Q上方时，求线段PQ的最大值.

（1）m=1，n=3；（2）S△BCD=21；（3）PQ的最大值为9. 【解析】试题分析： （1）把点A（-2，7）分别代入两个函数的解析式即可求得m=1，n=3； （2）由（1）中所得m=1可得抛物线的解析式为，令，求出对应的的值即可求得C、D的坐标；根据点A的坐标和AB∥轴交抛物线于点B，可求得点B的坐标，由此即可求出△BCD的面积； （3）由题意，可知P(t，-2 t...

在等腰△ABC中，AB=AC，将线段BA绕点B顺时针旋转到BD，使BD⊥AC于H，连结AD并延长交BC的延长线于点P.

(1)依题意补全图形；

(2)若∠BAC=2α，求∠BDA的大小（用含α的式子表示）；

(3)小明作了点D关于直线BC的对称点点E，从而用等式表示线段DP与BC之间的数量关系.请你用小明的思路补全图形并证明线段DP与BC之间的数量关系.

（1）补图见解析；（2）∠BDA=45°+α；（3）证明见解析. 【解析】试题分析： （1）按要求在图中画出相应图形即可； （2）由∠BAC=2α结合BD⊥AC于点H，可得∠ABH=90°-2α，再结合BD=AB即可求得∠BDA； （3）首先按要求补充完整图形，由点D和点E关于BP对称，可得BE=BD=AC，DE=2DG，DE⊥BP，∠DBP=∠EBP，结合（2）中结论，可...

在平面直角坐标系xOy中，点P的横坐标为x，纵坐标为2x，满足这样条件的点称为“关系点”.

(1)在点A(1,2)、B(2,1)、M(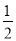，1)、N(1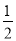， )中，是“关系点”的为 ；

(2)⊙O的半径为1，若在⊙O上存在“关系点”P，求点P坐标；

(3)点C的坐标为(3，0)，若在⊙C上有且只有一个“关系点”P，且“关系点”P的横坐标满足-2≤x≤2.请直接写出⊙C的半径r的取值范围．

（1）A、M；（2）或；（3）或. 【解析】试题分析： （1）由“关系点”的定义可知，关系点的纵坐标等于横坐标的2倍，由此可知四个点中A点和M点是“关系点”； （2）由题意按要求作半径为1的⊙O，如图1，在⊙O上取点P，根据关系点的定义设点P的坐标为（x，2x），过点P作PG⊥x轴于点G，在Rt△OPG中，由勾股定理建立方程，解方程求得x的值，即可得到点P的坐标； （3）“...

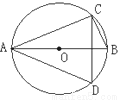
如图，AB是⊙O的直径，若∠BAC=35°，则∠ADC=（       ）

A. 35°                                       B. 55°                                       C. 70°                                       D. 110°

B 【解析】试题解析：∵AB是⊙O的直径， ∴∠ACB=90°， ∵∠BAC=35°， ∴∠ABC=180°-90°-35°=55°， ∴∠ADC=∠ABC=55°． 故选B．

下列命题中，正确命题的个数为（ ）

（1）三点确定一个圆 （2）平分弦的直径垂直于这条弦

（3）等弧对等弦 （4）直径是圆的对称轴

A．1 　　B．2 　 C．3 　 　 D．4

A 【解析】 试题分析：根据与圆有关的基本概念依次分析各小题即可作出判断. （1）不共线的三点确定一个圆，（2）在同圆中，平分弦的直径垂直于这条弦，（4）直径所再的直线是圆的对称轴，故错误； （3）等弧对等弦，正确； 故选A.

下列图形中，不是中心对称图形的是（　　）

A.                    B.                    C.                    D.

A 【解析】试题解析：A、不是中心对称图形，故本选项正确； B、是中心对称图形，故本选项错误； C、是中心对称图形，故本选项错误； D、是中心对称图形，故本选项错误； 故选A．

若二次根式 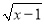在实数范围内有意义，则x的取值范围是（   ）

A. x≤﹣1 B. x≥1 C. x≤1 D. x≥1

D 【解析】试题解析：由题意得，x﹣1≥0， 解得x≥1． 故选D．