
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
已知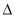 ABC与
ABC与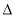 DEF相似,且
DEF相似,且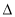 ABC与
ABC与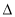 DEF的相似比为2:3,若
DEF的相似比为2:3,若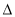 DEF 的面积为36,则
DEF 的面积为36,则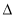 ABC的面积等于________.
ABC的面积等于________.
查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
已知线段AB=4,点P是线段AB的黄金分割点,且AP<BP,那么AP的长为_____.
(6﹣2)cm. 【解析】由题意得:BP2=AP·AB,BP=AB-AP, 即:(4-AP)2=4AP, 解得:AP= , 故答案为: .查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
若某斜面的坡度为1: 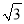 ,则该坡面的坡角为_____度.
,则该坡面的坡角为_____度.
查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
已知点A(﹣2,m)、B(2,n)都在抛物线y=x2+2x﹣t上,则m与n的大小关系是m_____n.(填“>”、“<”或“=”)
< 【解析】当x=-2时,y=-t,即m=-t, 当x=2时,y=8-t,即n=8-t, -t<8-t,所以m查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
如图,在Rt△ABC中,∠BAC=90°,点G是重心,联结AG,过点G作DG∥BC,DG交AB于点D,若AB=6,BC=9,则△ADG的周长等于_____.
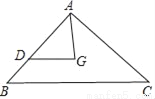
查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
已知⊙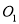 的半径为4,⊙
的半径为4,⊙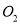 的半径为R,若⊙
的半径为R,若⊙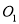 与⊙
与⊙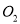 相切,且
相切,且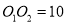 ,则R的值为________.
,则R的值为________.
查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
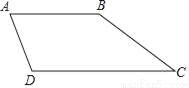
如果一个四边形的某个顶点到其他三个顶点的距离相等,我们把这个四边形叫做等距四边形,这个顶点叫做这个四边形的等距点.如图,已知梯形ABCD是等距四边形,AB∥CD,点B是等距点.若BC=10,cosA=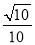 ,则CD的长等于_____.
,则CD的长等于_____.
查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:填空题
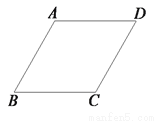
如图,在边长为2的菱形ABCD中, 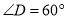 ,点E、F分别在边AB、BC上. 将
,点E、F分别在边AB、BC上. 将 BEF沿着直线EF翻折,点B恰好与边AD的中点G重合,则BE的长等于________.
BEF沿着直线EF翻折,点B恰好与边AD的中点G重合,则BE的长等于________.
查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:解答题
计算: 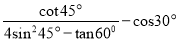 .
.
查看答案和解析>>
科目: 来源:上海市长宁区2018届九年级上学期期末质量检测数学试卷 题型:解答题
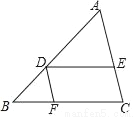
如图,在△ABC中,点D在边AB上,DE∥BC,DF∥AC,DE、DF分别交边AC、BC于点E、F,且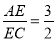 .
.
(1)求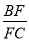 的值;
的值;
(2)联结EF,设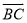 =
=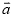 ,
, 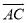 =
=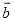 ,用含
,用含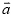 、
、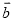 的式子表示
的式子表示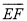 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com