
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:填空题
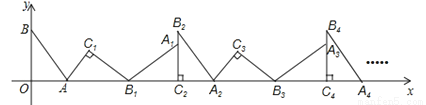
如图,在平面直角坐标系中,将△ABO绕点A顺时针旋转到△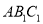 的位置,点B,O分别落在点
的位置,点B,O分别落在点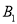 ,
,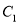 处,点
处,点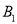 在
在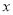 轴上,再将△
轴上,再将△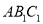 绕点
绕点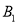 顺时针旋转到△
顺时针旋转到△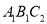 的位置,点
的位置,点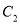 在
在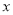 轴上,将△
轴上,将△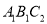 绕点
绕点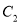 顺时针旋转△
顺时针旋转△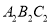 的位置,点
的位置,点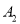 在
在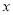 轴上……依次进行下去。若点
轴上……依次进行下去。若点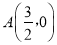 ,B(0,2),则点
,B(0,2),则点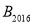 的坐标为_____________ .
的坐标为_____________ .
查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
解方程: 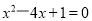
查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
已知抛物线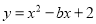 经过点A(-2,8).
经过点A(-2,8).
(1)求此抛物线的函数解析式,并写出此抛物线的对称轴;
(2)判断点B(-1,-4)是否在此抛物线上.
(1)抛物线的函数解析式为,对称轴为直线; (2)点B(-1,-4)不在此抛物线上,理由见解析. 【解析】试题分析:(1)把A(-2,8)代入,即可求出b的值,再根据对称轴公式,求出对称轴; (2)把B(-1,-4)代入,若左右两边的值相等,则点在函数图像上,反之则不在函数图像上. 【解析】 (1)将点A(-2,8)代入 得 解得 ∴抛物线的函数解析式为...查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
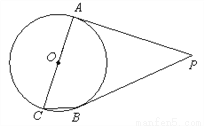
如图,PA,PB是⊙O的切线,点A,B为切点,AC是⊙O的直径,∠ACB=70°,求∠APB的度数.
查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
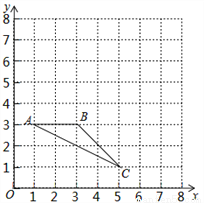
已知△ABC在平面直角坐标系中的位置如图所示:
(1)画出△ABC绕点A按逆时针方向旋转90°后的△A′B′C′;
(2)在(1)的条件下,求点C旋转到点C′所经过的路线长及线段AC旋转到新位置时所划过区域的面积.
查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
不透明的口袋里装有白、黄、蓝三种颜色的乒乓球(除颜色外其余都相同),其中白球有2个,黄球有1个,再从中任意摸出1个球是白球的概率为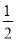 .
.
(1)试求袋中蓝球的个数;
(2)第一次任意摸出一个球(不放回),第二次再摸出一个球,请用树状图或列表法表示两次摸到球的所有可能结果,并求两次摸到的球都是白球的概率.
(1)蓝球有1个;(2) 【解析】试题分析:(1)先根据白球的概率是,可求出球的总数,然后用求得的球的总个数减去白球和黄球的个数即可; (2)画出树状图可知,共有12种可能结果,两次摸到的球都为白球的情况有2种,从而可求出两次摸到的球都是白球的概率. 【解析】 (1)总球数为个,4-2-1=1 ∴蓝球有1个 (2) 开始 第一次 白1 白2 黄 蓝 第二...查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
某蔬菜有限公司一年四季都有大量新鲜蔬菜销往全国各地,近年来它的蔬菜产值不断增加,2014年蔬菜的产值是640万元,2016年产值达到1000万元.
(1)求2015年、2016年蔬菜产值的平均增长率是多少?
(2)若2017年蔬菜产值继续稳定增长(即年增长率与前两年的年增长率相同),那么请你估计2017年该公司的蔬菜产值达到多少万元?
(1)2015、2016年蔬菜产值的年平均增长率为25%; (2)2017年该公司的蔬菜产值将达到1250万元. 【解析】试题分析:对于(1),设2015年、2016年蔬菜产值的年平均增长率为x,则2015年的产值是640(1+x)万元,2016年的产值是640(1+x)2万元,结合2016年产值达到1000万元列方程求解; 对于(2),根据(1)求解的结果,进一步列式1000×...查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
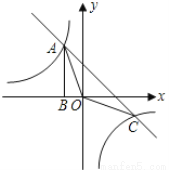
如图,Rt△ABO的顶点A是双曲线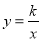 与直线
与直线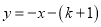 在第二象限的交点,AB⊥
在第二象限的交点,AB⊥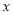 轴于点B且S△ABO=
轴于点B且S△ABO=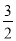 .
.
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A,C的坐标;
(3)求△AOC的面积.
查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
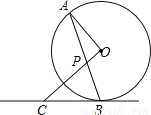
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为3,OP=1,求BC的长.
查看答案和解析>>
科目: 来源:广东省江门市江海区五校2018届九年级上学期期末联考数学试卷 题型:解答题
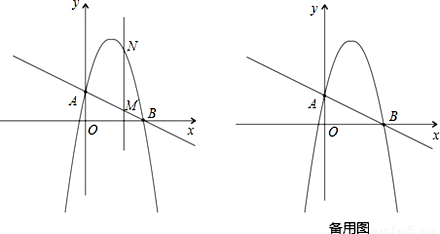
如图,一次函数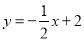 分别交y轴、x 轴于A、B两点,抛物线
分别交y轴、x 轴于A、B两点,抛物线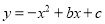 过A、B两点.
过A、B两点.
(1)求这个抛物线的解析式;
(2)作垂直x轴的直线x=t,在第一象限交直线AB于点M,交这个抛物线于点N.求当t 取何值时,MN有最大值?最大值是多少?
(3)在(2)的情况下,以A、M、N、D为顶点作平行四边形,求第四个顶点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com