
科目: 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
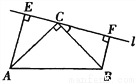
如图,在△ABC中,∠ACB=90°,AC=BC,直线l经过顶点C,过A、B两点分别作l的垂线AE、BF,E、F为垂足.当直线l不与底边AB相交时,
求证:EF=AE+BF.
查看答案和解析>>
科目: 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
记y= f(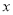 )=
)=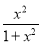 . 如: f(1)表示当x=1时y的值,即f(1)=
. 如: f(1)表示当x=1时y的值,即f(1)=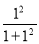 =
=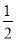 ;f(
;f(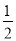 )表示当
)表示当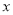 =
=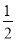 时y的值,即f(
时y的值,即f(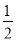 )=
)=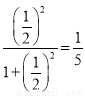 .
.
试回答:
(1)f(1)+f(2)+f(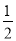 )+f(3)+f(
)+f(3)+f(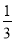 )=__________ ;
)=__________ ;
(2)f(1)+f(2)+f(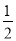 )+f(3)+f(
)+f(3)+f(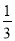 )+……+f(
)+……+f(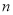 )+f(
)+f(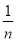 )=__________.(结果用含
)=__________.(结果用含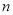 的代数式表示,
的代数式表示, 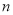 为正整数)
为正整数)
查看答案和解析>>
科目: 来源:北京市2017-2018学年第一学期八年级数学期中试卷 题型:解答题
阅读下列材料
通过小学的学习我们知道,分数可分为“真分数”和“假分数”.而假分数都可化为带分数,如: 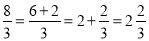 .
.
我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
如: 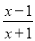 ,
, 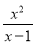 这样的分式就是假分式;再如:
这样的分式就是假分式;再如: 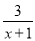 ,
, 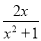 这样的分式就是真分式.
这样的分式就是真分式.
类似的,假分式也可以化为带分式(即:整式与真分式的和的形式).
如: 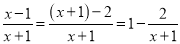 ;
; 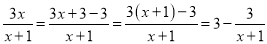 ;
;
再如: 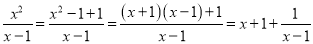 .
.
解决下列问题:
(1)分式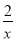 是 分式(填“真分式”或“假分式”);
是 分式(填“真分式”或“假分式”);
(2)假分式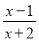 可化为带分式 的形式;
可化为带分式 的形式;
(3)如果分式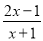 的值为整数,那么x的整数值为 .
的值为整数,那么x的整数值为 .
查看答案和解析>>
科目: 来源:北京市燕山区2018届初三第一学期期末数学试卷 题型:解答题
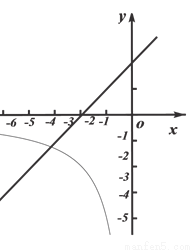
如图,在平面直角坐标系xoy中,函数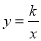 (x<0)的图象与直线y=x+2交于点A(-3,m).
(x<0)的图象与直线y=x+2交于点A(-3,m).
(1)求k,m的值;
(2)已知点P(a,b)是直线y=x上,位于第三象限的点,过点P作平行于x轴的直线,交直线y=x+2于点M,过点P作平行于y轴的直线,交函数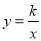 (x<0)的图象于点N.
(x<0)的图象于点N.
①当a=-1时,判断线段PM与PN的数量关系,并说明理由;
②若PN≥PM结合函数的图象,直接写出b的取值范围.
查看答案和解析>>
科目: 来源:北京市燕山区2018届初三第一学期期末数学试卷 题型:解答题
阅读下列材料:
实验数据显示,一般成人喝250毫升低度白酒后,其血液中酒精含量(毫克/百毫升)随时间的增加逐步增高达到峰值,之后血液中酒精含量随时间的增加逐渐降低.
小带根据相关数据和学习函数的经验,对血液中酒精含量随时间变化的规律进行了探究,发现血液中酒精含量y是时间x的函数,其中y表示血液中酒精含量(毫克/百毫升),x表示饮酒后的时间(小时).
下表记录了6小时内11个时间点血液中酒精含量y(毫克/百毫升)随饮酒后的时间x(小时)(x>0)的变化情况.
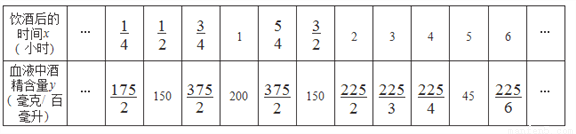
下面是小带的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,以上表中各对数值为坐标描点,图中已给出部分点,请你描出剩余的点,画出血液中酒精含量y随时间x变化的函数图象;
(2)观察表中数据及图象可发现此函数图象在直线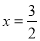 两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;
两侧可以用不同的函数表达式表示,请你任选其中一部分写出表达式;
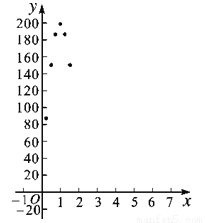
(3)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:30在家喝完250毫升低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
(1)答案见解析;(2)(0<x≤)或(x>);(3)不能. 【解析】试题分析:(1)利用描点法画出函数图象即可; (2)利用待定系数法即可解决问题; (3)把y=20代入反比例函数y=得x=11.25.喝完酒经过11.25小时为早上7:45,即早上7:45以后血液中的酒精含量小于或等于20毫克/百毫升.由此即可判断. 试题解析:(1)图象如图所示. (2)y=-20...查看答案和解析>>
科目: 来源:北京市燕山区2018届初三第一学期期末数学试卷 题型:解答题
在平面直角坐标系xOy中,反比例函数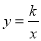 的图象经过点A(1,4),B(m,n).
的图象经过点A(1,4),B(m,n).
(1)求反比例函数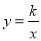 的解析式;
的解析式;
(2)若二次函数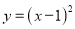 的图象经过点B,求代数式
的图象经过点B,求代数式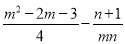 的值;
的值;
(3)若反比例函数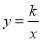 的图象与二次函数
的图象与二次函数 的图象只有一个交点,且该交点在直线y=x的下方,结合函数图象,求a的取值范围.
的图象只有一个交点,且该交点在直线y=x的下方,结合函数图象,求a的取值范围.
查看答案和解析>>
科目: 来源:北京市燕山区2018届初三第一学期期末数学试卷 题型:解答题
在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.
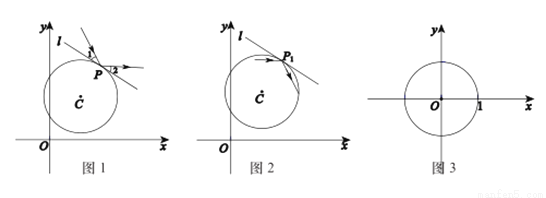
(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线和反射点P3;
(2)当⊙O的半径为1时,如图3:
①第一象限内的一条入射光线平行于y轴,且自⊙O的外部照射在圆上点P处,此光线经⊙O反射后,反射光线与x轴平行,则反射光线与切线l的夹角为___________°;
②自点M(0,1)出发的入射光线,在⊙O内顺时针方向不断地反射.若第1个反射点是P1,第二个反射点是P2,以此类推,第8个反射点是P8恰好与点M重合,则第1个反射点P1的坐标为___________;
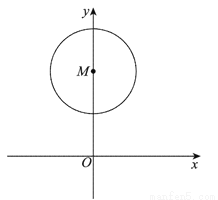
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.
查看答案和解析>>
科目: 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:单选题
-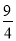 和(-
和(-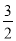 )2的关系是( )
)2的关系是( )
A. 相等 B. 互为相反数 C. 互为倒数 D. 上述答案都不正确
B 【解析】根据乘方运算的性质,可知(-)2=,故它们互为相反数. 故选:B.查看答案和解析>>
科目: 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:单选题
下列几何体是由4个相同的小正方体搭成的,其中左视图与俯视图相同的是( )
A. 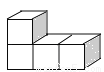 B.
B. 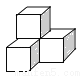 C.
C. 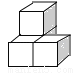 D.
D. 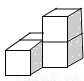
查看答案和解析>>
科目: 来源:2017-2018学年陕西安市九年级(上)期末数学试卷 题型:单选题
已知一元二次方程ax2+bx+c=0(a≠0)中,下列说法:
①若a+b+c=0,则b2﹣4ac>0;
②若方程两根为﹣1和2,则2a+c=0;
③若方程ax2+c=0有两个不相等的实根,则方程ax2+bx+c=0必有两个不相等的实根;
④若b=2a+c,则方程有两个不相等的实根.其中正确的有( )
A. ①②③ B. ①②④ C. ②③④ D. ①②③④
C 【解析】试题解析:①当时,有若 即方程有实数根了, 故错误; ②把 代入方程得到:(1) 把代入方程得到: (2) 把(2)式减去(1)式×2得到: 即: 故正确; ③方程 有两个不相等的实数根, 则它的 而方程的 ∴必有两个不相等的实数根.故正确; ④若则 故正确. ②③④都正确, 故选C.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com