
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:填空题
如果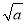 的平方根是±3,则
的平方根是±3,则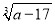 =__________.
=__________.
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:填空题
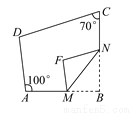
如图,四边形ABCD中,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,则∠B=__________.
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:填空题
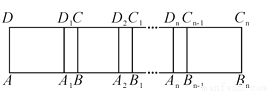
如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 016,则n的值为__________.
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
计算:
(1)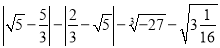 ;(2)
;(2)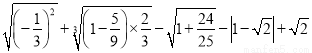 .
.
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
已知3a-2的平方根是±5,4a-2b-8的算术平方根是4,求a+3b的立方根.
3. 【解析】根据题意可以求得a、b的值,再求a+3b的立方根即可. 【解析】 ∵3a-2的平方根是±5, ∴3a-2=25,解得a=9. ∵4a-2b-8的算术平方根是4, ∴36-2b-8=16, 解得b=6, ∴a+3b=9+3×6=27. ∴a+3b的立方根为3.查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
在如图所示的平面直角坐标系中表示下面各点:A(0,3),B(1,-3),C(3,-5),D(-3,-5),E(3,5),F(5,6),G(5,0).
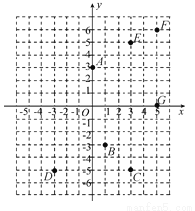
(1)将点C向x轴的负方向平移6个单位长度,它与点__ __重合;
(2)连接CE,则直线CE与y轴是什么关系?
(1)答案见解析;(2)CE∥y轴. 【解析】(1)将点C向x轴的负方向平移6个单位得到对应点的坐标为(-3,-5),于是可判断它与点D重合. (2)利用点C和点E的横坐标相同可判断直线CE与坐标轴的关系; 【解析】 (1)将点C向x轴的负方向平移6个单位,它与点D重合; (2)直线CE与y轴平行.查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
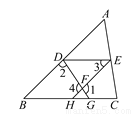
如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
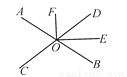
如图,两直线AB,CD相交于点O,OE平分∠BOD,∠AOC∶∠AOD=7∶11.
(1)求∠COE的度数;
(2)若OF⊥OE,求∠COF的度数.
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
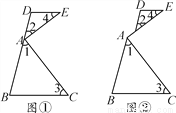
如图,∠EAC=90°,∠1+∠2=90°,∠1=∠3,∠2=∠4.
(1)如图①,求证:DE∥BC;
(2)若将图①改变为图②,其他条件不变,(1)中的结论是否仍成立?请说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年七年级数学下册(人教版):期中检测题 题型:解答题
有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
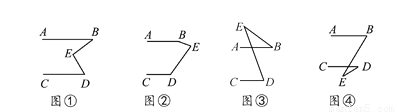
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
(1)(1)图①:∠BED=∠B+∠D;图②:∠B+∠BED+∠D=360°;图③:∠BED=∠D-∠B;图④:∠BED=∠B-∠D;(2)证明见解析. 【解析】(1)根据两直线平行,内错角相等,即可解答; (2)选择③,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠DEF-∠BEF即可证明. 【解析】 (1)图①:∠BED...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com