
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:填空题
如图,已知AD∥EF∥BC,如果AE=2EB,DF=6,那么CD的长为_____.
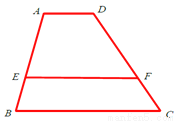
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:填空题
在Rt△ABC中,∠C=90°,如果AB=6, 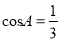 ,那么AC=_____.
,那么AC=_____.
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:填空题
如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线分别交边BC、AB于点D、E如果BC=8, 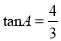 ,那么BD=_____.
,那么BD=_____.
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:填空题
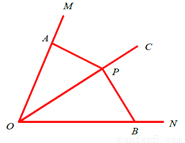
如图,点P为∠MON平分线OC上一点,以点P为顶点的∠APB两边分别与射线OM、ON相交于点A、B,如果∠APB在绕点P旋转时始终满足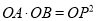 ,我们就把∠APB叫做∠MON的关联角.如果∠MON=50°,∠APB是∠MON的关联角,那么∠APB的度数为____.
,我们就把∠APB叫做∠MON的关联角.如果∠MON=50°,∠APB是∠MON的关联角,那么∠APB的度数为____.
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:填空题
在Rt△ABC中,∠C=90°,AC=6,BC=8(如图),点D是边AB上一点,把△ABC绕着点D旋转90°得到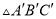 ,边
,边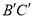 与边AB相交于点E,如果AD=BE,那么AD长为____.
与边AB相交于点E,如果AD=BE,那么AD长为____.
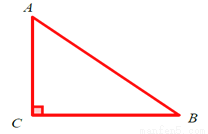
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:解答题
计算: 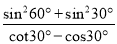 .
.
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:解答题
小明按照列表、描点、连线的过程画二次函数的图像,下表与下图是他所完成的部分表格与图像,求该二次函数的解析式,并补全表格与图像.

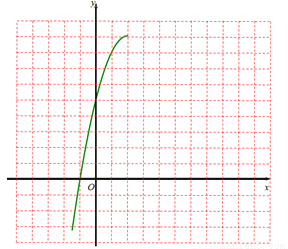
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:解答题
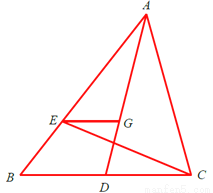
如图,在△ABC中,点E在边AB上,点G是△ABC的重心,联结AG并延长交BC于点D.
(1)若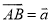 ,
, 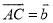 ,用向量
,用向量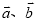 表示向量
表示向量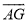 ;
;
(2)若∠B=∠ACE,AB=6, 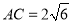 ,BC=9,求EG的长.
,BC=9,求EG的长.
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:解答题
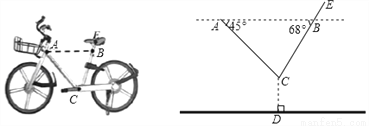
如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
查看答案和解析>>
科目: 来源:上海市虹口区2017学年九年级第一学期期终教学质量监控测试 题型:解答题
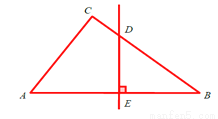
如图,在△ABC中,点D、E分别在边AB、AC上,DE、BC的延长线相交于点F,且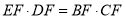 .
.
(1)求证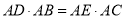 ;
;
(2)当AB=12,AC=9,AE=8时,求BD的长与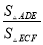 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com