
科目: 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
解方程:x2-x-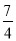 =0
=0
查看答案和解析>>
科目: 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
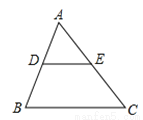
如图,在△ABC中,DE∥BC中,AD=1,BD=2,DE=2求BC的长
查看答案和解析>>
科目: 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DF
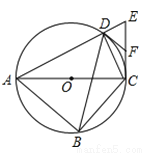
(1)求∠CDE的度数
(2)求证:DF是⊙O的切线
证明见解析 【解析】试题分析:(1)直接利用圆周角定理得出∠CDE的度数; (2)直接利用直角三角形的性质结合等腰三角形的性质得出∠ODF=∠ODC+∠FDC=∠OCD+∠DCF=90°,进而得出答案. 试题解析:(1)∵对角线AC为⊙O的直径, ∴∠ADC=90°, ∴∠EDC=90°; (2)连接DO, ∵∠EDC=90°,F是EC的中点,∴DF=FC...查看答案和解析>>
科目: 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
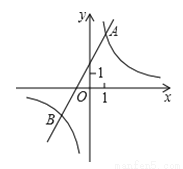
已知反比例函数y1=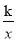 的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
的图象与一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2) .
(1)求这两个函数的关系式;
(2)观察图象,直接写出使得y1>y2成立的自变量x的取值范围.
查看答案和解析>>
科目: 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=一的图象上一部分,请根据图中信息解答下列问题
(1)恒温系统在这天保持大棚内温度20℃的时间有多少小时?
(2)求k的值;
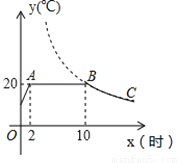
(3)当x=20时,大棚内的温度约为多少度?
(1)8小时;(2)200;(3)当x=20时,大棚内的温度约为10℃. 【解析】试题分析:(1)根据图象直接得出大棚温度20℃的时间为10﹣2=8(小时); (2)利用待定系数法求反比例函数解析式即可; (3)将x=20代入函数解析式求出y的值即可. 试题解析:(1)恒温系统在这天保持大棚温度20℃的时间为:10﹣2=8(小时); (2)∵点B(10,20)在双曲线...查看答案和解析>>
科目: 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为20℃的条件下生长最快的新品种.图示是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是反比例函数y=一的图象上一部分,请根据图中信息解答下列问题
(1)恒温系统在这天保持大棚内温度20℃的时间有多少小时?
(2)求k的值;
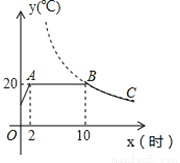
(3)当x=20时,大棚内的温度约为多少度?
【答案】(1)8小时;(2)200;(3)当x=20时,大棚内的温度约为10℃.
【解析】试题分析:(1)根据图象直接得出大棚温度20℃的时间为10﹣2=8(小时);
(2)利用待定系数法求反比例函数解析式即可;
(3)将x=20代入函数解析式求出y的值即可.
试题解析:(1)恒温系统在这天保持大棚温度20℃的时间为:10﹣2=8(小时);
(2)∵点B(10,20)在双曲线y=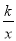 上,
上,
∴20=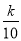 ,
,
∴解得:k=200;
(3)当x=20时,y=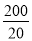 =10,
=10,
所以当x=20时,大棚内的温度约为10℃.
【点睛】本题考查了反比例函数的应用,正确地求得反比例函数的解析式是解题的关键.
【题型】解答题
【结束】
25
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB=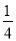 (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
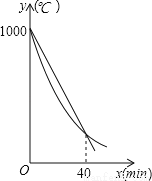
(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
(1)yA=﹣20x+1000; (2)B组材料的温度是164℃; (3)当x=20时,两组材料温差最大为100℃. 【解析】试题分析:(1)首先求出yB函数关系式,进而得出交点坐标,即可得出yA函数关系式;(2)首先将y=120代入求出x的值,进而代入yB求出答案;(3)得出yA-yB的函数关系式,进而求出最值即可. 试题解析:(1)由题意可得出:yB=(x﹣60)2+m...查看答案和解析>>
科目: 来源:河北省唐山市路北区2017-2018学年度第一学期学生素质终期评价九年级数学 题型:解答题
某研究所将某种材料加热到1000℃时停止加热,并立即将材料分为A、B两组,采用不同工艺做降温对比实验,设降温开始后经过x min时,A、B两组材料的温度分别为yA℃、yB℃,yA、yB与x的函数关系式分别为yA=kx+b,yB= (x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.
(x﹣60)2+m(部分图象如图所示),当x=40时,两组材料的温度相同.

(1)分别求yA、yB关于x的函数关系式;
(2)当A组材料的温度降至120℃时,B组材料的温度是多少?
(3)在0<x<40的什么时刻,两组材料温差最大?
【答案】(1)yA=﹣20x+1000;
(2)B组材料的温度是164℃;
(3)当x=20时,两组材料温差最大为100℃.
【解析】试题分析:(1)首先求出yB函数关系式,进而得出交点坐标,即可得出yA函数关系式;(2)首先将y=120代入求出x的值,进而代入yB求出答案;(3)得出yA-yB的函数关系式,进而求出最值即可.
试题解析:(1)由题意可得出:yB= (x﹣60)2+m经过(0,1000),
(x﹣60)2+m经过(0,1000),
则1000= (0﹣60)2+m,
(0﹣60)2+m,
解得:m=100,
∴yB= (x﹣60)2+100,
(x﹣60)2+100,
当x=40时,yB= ×(40﹣60)2+100,
×(40﹣60)2+100,
解得:yB=200,
yA=kx+b,经过(0,1000),(40,200),
则 ,
,
解得:  ,
,
∴yA=﹣20x+1000;
(2)当A组材料的温度降至120℃时,
120=﹣20x+1000,
解得:x=44,
当x=44,yB= (44﹣60)2+100=164(℃),
(44﹣60)2+100=164(℃),
∴B组材料的温度是164℃;
(3)当0<x<40时,yA﹣yB=﹣20x+1000﹣ (x﹣60)2﹣100=﹣
(x﹣60)2﹣100=﹣ x2+10x=﹣
x2+10x=﹣ (x﹣20)2+100,
(x﹣20)2+100,
∴当x=20时,两组材料温差最大为100℃.
【题型】解答题
【结束】
26
正方形ABCD的边长为6cm,点E,M分别是线段BD,AD上的动点,连接AE并延长,交边BC于F,过M作MN⊥AF,垂足为H,交边AB于点N.
(1)如图①,若点M与点D重合,求证:AF=MN;
(2)如图②,若点M从点D出发,以1cm/s的速度沿DA向点A运动,同时点E从点B出发,以 cm/s的速度沿BD向点D运动,运动时间为ts.
cm/s的速度沿BD向点D运动,运动时间为ts.
①设BF=ycm,求y关于t的函数表达式;
②当BN=2AN时,连接FN,求FN的长.

查看答案和解析>>
科目: 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:单选题
三角形的内角和是( )
A. 60° B. 90° C. 180° D. 360°
C 【解析】试题解析:∵三角形的内角和是180° 故选C.查看答案和解析>>
科目: 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:单选题
3的算术平方根是( )
A. -3 B. 3 C. -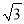 D.
D. 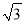
查看答案和解析>>
科目: 来源:2017-2018年福建厦门市八年级上册数学期末质量检测试卷 题型:单选题
如图,在直角三角形ABC中,∠C=90°,∠B=60°,BC=a,AC=b,则AB的长是( )

A. 2b B. 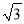 b C.
b C. 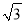 a D. 2a
a D. 2a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com