
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:填空题
请写出“等腰三角形的两底角相等”的逆命题:__________.
有两个角相等的三角形是等腰三角形 【解析】∵原命题的题设是:“一个三角形是等腰三角形”,结论是“这个三角形两底角相等”, ∴命题“等腰三角形的两个底角相等”的逆命题是“有两个角相等的三角形是等腰三角形”, 故答案为:有两个角相等的三角形是等腰三角形.查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:填空题
等腰三角形的一个内角是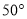 ,则它的底角是__________.
,则它的底角是__________.
查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:填空题
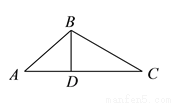
如图,在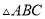 中,
中, 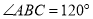 ,
, 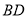 是
是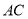 边上的高,若
边上的高,若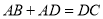 ,则
,则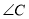 等于__________.
等于__________.
查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:填空题
如图,在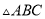 中,
中, 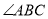 和
和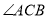 的平分线相交于点
的平分线相交于点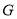 ,过点
,过点 作
作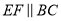 交
交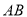 于
于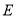 ,交
,交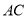 于
于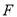 ,过点
,过点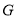 作
作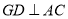 于
于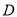 ,下列四个结论:①
,下列四个结论:①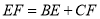 ;②
;②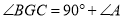 ;③点
;③点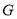 到
到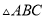 各边的距离相等;④设
各边的距离相等;④设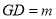 ,
, 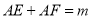 ,则
,则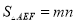 .其中正确的结论是__________.
.其中正确的结论是__________.
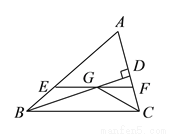
查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
解不等式:(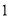 )
)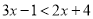 . (
. (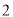 )
)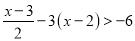 .
.
查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
如图,在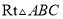 中,
中, 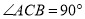 .
.
(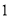 )用尺规在边
)用尺规在边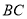 上求作一点
上求作一点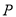 ,使
,使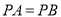 (不写作法,保留作图痕迹).
(不写作法,保留作图痕迹).
(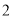 )连结
)连结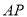 ,若
,若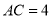 ,
, 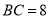 ,试求
,试求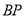 的长.
的长.

查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
如图,在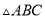 中,
中, 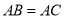 ,点
,点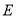 在
在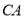 延长线上,
延长线上, 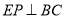 于点
于点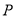 ,交
,交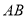 于点
于点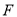 .
.
( )求证:
)求证: 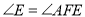 .
.
( )若
)若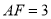 ,
, 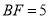 ,求
,求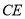 的长.
的长.

查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
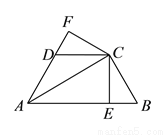
如图,已知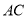 平分
平分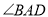 ,
, 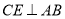 于
于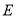 ,
, 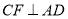 于
于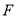 ,且
,且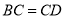 .
.
( )求证:
)求证: 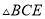 ≌
≌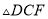 .
.
( )若
)若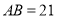 ,
, 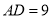 ,
, 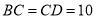 ,求
,求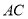 的长.
的长.
查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
在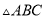 中,
中, 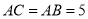 ,一边上高为
,一边上高为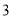 ,求底边
,求底边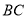 的长(注意:请画出图形).
的长(注意:请画出图形).
查看答案和解析>>
科目: 来源:浙江杭州西湖区保俶塔实验学校2017-2018学年八年级上学期期中数学试卷 题型:解答题
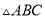 是一张等腰直角三角形纸板,
是一张等腰直角三角形纸板, 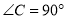 ,
, 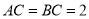 .
.
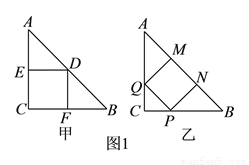
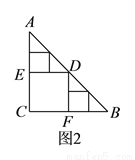
( )要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图
)要在这张纸板中剪出一个尽可能大的正方形,有甲、乙两种剪法(如图 ),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
),比较甲、乙两种剪法,哪种剪法所得的正方形面积大?请说明理由.
( )图
)图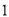 中甲种剪法称为第
中甲种剪法称为第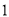 次剪取,记所得正方形面积为
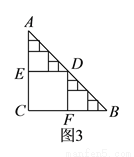
次剪取,记所得正方形面积为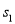 ;按照甲种剪法,在余下的
;按照甲种剪法,在余下的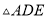 和
和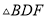 中,分别剪取正方形,得到两个相同的正方形,称为第
中,分别剪取正方形,得到两个相同的正方形,称为第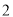 次剪取,并记这两个正方形面积和为
次剪取,并记这两个正方形面积和为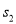 (如图
(如图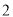 ),则
),则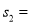 __________;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第
__________;再在余下的四个三角形中,用同样方法分别剪取正方形,得到四个相同的正方形,称为第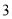 次剪取,并记这四个正方形面积和为
次剪取,并记这四个正方形面积和为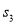 ,继续操作下去,则第
,继续操作下去,则第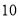 次剪取时,
次剪取时, 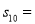 __________.
__________.
(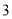 )求第
)求第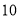 次剪取后,余下的所有小三角形的面积之和__________.
次剪取后,余下的所有小三角形的面积之和__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com