
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
已知△ABC,AB=AC,BC=8,点D、E分别在边BC、AB上,将△ABC沿着直线DE翻折,点B落在边AC上的点M处,且AC=4AM,设BD=m,那么∠ACB的正切值是_____.(用含m的代数式表示)
【解析】如图所示:作AH⊥BC,MG⊥BC,连结EM、MC. ∵AB=AC,BC=8,AH⊥BC, ∴CH=4. ∵AC=4AM, ∴CM:AC=3:4. ∵AH∥MG, ∴,即,解得:CG=3. ∴BG=5. ∴DG=m﹣5. 由翻折的性质可知MD=BD=m. 在Rt△MGD中,依据勾股定理可知:MG=. ∴tan∠ACB=. ...查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
已知抛物线y=﹣2x2﹣4x+1.
(1)求这个抛物线的对称轴和顶点坐标;
(2)将这个抛物线平移,使顶点移到点P(2,0)的位置,写出所得新抛物线的表达式和平移的过程.
(1)对称轴是直线x=﹣1,顶点坐标为(﹣1,3);(2)y=﹣2(x﹣2)2,平移过程为:向右平移3个单位,向下平移3个单位. 【解析】试题分析:(1)根据配方法的操作进行整理即可得解; (2)根据顶点写出新的顶点式形式,再根据顶点的变化确定平移方法. 试题解析:(1)y=﹣2x2﹣4x+1, =﹣2(x2+2x+1)+2+1, =﹣2(x+1)2+3, 所以,对...查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
已知:如图,在平行四边形ABCD中,AD=2,点E是边BC的中点,AE、BD相交于点F,过点F作FG∥BC,交边DC于点G.
(1)求FG的长;
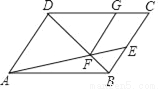
(2)设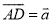 ,
, 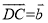 ,用
,用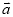 、
、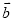 的线性组合表示
的线性组合表示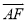 .
.
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
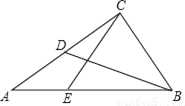
已知:如图,在Rt△ABC中,∠ACB=90°,BC=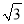 ,cot∠ABC=
,cot∠ABC=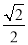 ,点D是AC的中点.
,点D是AC的中点.
(1)求线段BD的长;
(2)点E在边AB上,且CE=CB,求△ACE的面积.
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
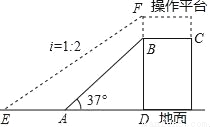
如图,为了将货物装入大型的集装箱卡车,需要利用传送带AB将货物从地面传送到高1.8米(即BD=1.8米)的操作平台BC上.已知传送带AB与地面所成斜坡的坡角∠BAD=37°.
(1)求传送带AB的长度;
(2)因实际需要,现在操作平台和传送带进行改造,如图中虚线所示,操作平台加高0.2米(即BF=0.2米),传送带与地面所成斜坡的坡度i=1:2.求改造后传送带EF的长度.(精确到0.1米)(参考数值:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, 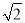 ≈1.41,
≈1.41, 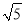 ≈2.24)
≈2.24)
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
已知:如图,四边形ABCD,∠DCB=90°,对角线BD⊥AD,点E是边AB的中点,CE与BD相交于点F,BD2=AB•BC
(1)求证:BD平分∠ABC;
(2)求证:BE•CF=BC•EF.
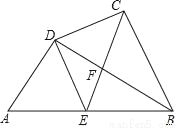
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
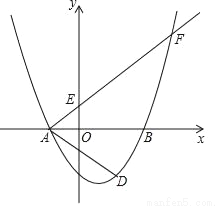
如图,在平面直角坐标系xOy中,已知抛物线y= 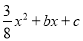 与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且
与x轴交于点A(﹣2,0)和点B,与y轴交于点C(0,﹣3),经过点A的射线AM与y轴相交于点E,与抛物线的另一个交点为F,且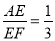 .
.
(1)求这条抛物线的表达式,并写出它的对称轴;
(2)求∠FAB的余切值;
(3)点D是点C关于抛物线对称轴的对称点,点P是y轴上一点,且∠AFP=∠DAB,求点P的坐标.
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:解答题
已知:如图,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,点E在边AD上(不与点A、D重合),∠CEB=45°,EB与对角线AC相交于点F,设DE=x.
(1)用含x的代数式表示线段CF的长;
(2)如果把△CAE的周长记作C△CAE,△BAF的周长记作C△BAF,设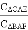 =y,求y关于x的函数关系式,并写出它的定义域;
=y,求y关于x的函数关系式,并写出它的定义域;
(3)当∠ABE的正切值是 时,求AB的长.
时,求AB的长.
查看答案和解析>>
科目: 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
如图所示的图案中,有2条对称轴的轴对称图形是( )
A. 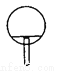
B. 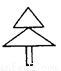
C. 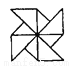
D. 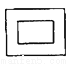
查看答案和解析>>
科目: 来源:广东省潮州市潮安区2017-2018学年八年级上学期期末教学质量检测数学试卷 题型:单选题
下列运算正确的是( )
A. 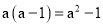 B.
B. 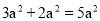
C. 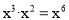 D.
D. 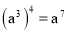
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com