
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
计算:tan60°﹣cos30°=_____.
【解析】根据特殊角的三角函数值,直接计算即可得tan60°﹣cos30°==. 故答案为: .查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如果抛物线y=ax2+5的顶点是它的最低点,那么a的取值范围是_____.
a>0 【解析】根据二次函数的图像,由抛物线y=ax2+5的顶点是它的最低点,知a>0, 故答案为a>0.查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如果抛物线y=2x2与抛物线y=ax2关于x轴对称,那么a的值是_____.
-2 【解析】根据关于x轴对称的抛物线的开口方向改变,开口大小不变,可由抛物线y=2x2与抛物线y=ax2关于x轴对称,知两抛物线开口大小不变,方向相反,因此可得a=﹣2. 故答案为:﹣2.查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如果向量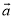 、
、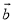 、
、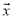 满足关系式4
满足关系式4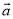 ﹣(
﹣(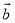 ﹣
﹣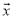 )=
)=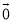 ,那么
,那么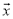 =_____.(用向量
=_____.(用向量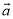 、
、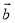 表示)
表示)
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
某快递公司十月份快递件数是10万件,如果该公司第四季度每个月快递件数的增长率都为x(x>0),十二月份的快递件数为y万件,那么y关于x的函数解析式是_____.
y=10(x+1)2 【解析】根据题意,把十月份的看作单位1,进而可得十二月邮件数为:y=10(x+1)2,所以y关于x的函数解析式是y=10(x+1)2. 故答案为:y=10(x+1)2查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
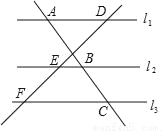
如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,已知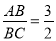 ,则
,则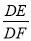 的值为_____.
的值为_____.
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
如果两个相似三角形的面积的比是4:9,那么它们对应的角平分线的比是_____.
2:3 【解析】先根据相似三角形面积的比是4:9,求出其相似比是2:3,再根据其对应的角平分线的比等于相似比,可知它们对应的角平分线比是2:3. 故答案为:2:3.查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
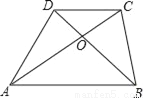
如图,已知梯形ABCD中,AB∥CD,对角线AC、BD相交于点O,如果S△AOB=2S△AOD,AB=10,那么CD的长是_____.
查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
已知AD、BE是△ABC的中线,AD、BE相交于点F,如果AD=6,那么AF的长是_____.
4 【解析】由三角形的重心的概念和性质,由AD、BE为△ABC的中线,且AD与BE相交于点F,可知F点是三角形ABC的重心,可得AF=AD=×6=4. 故答案为:4.查看答案和解析>>
科目: 来源:2018年上海市奉贤区中考数学一模试卷 题型:填空题
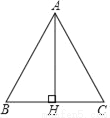
如图,在△ABC中,AB=AC,AH⊥BC,垂足为点H,如果AH=BC,那么sin∠BAC的值是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com