
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
(本题满分8分)解方程:
(1)计算: 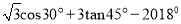 ;
;
(2)解方程: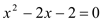 .
.
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
在“爱满扬州”慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成统计图.
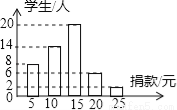
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)求这50名同学捐款的平均数;
(3)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
(1)15,15;(2)13(元);(3)7800(元). 【解析】试题分析:(1)根据众数的定义即出现次数最多的数据进而得出即可,再利用中位数的定义得出即可; (2)利用条形统计图得出各组频数,再根据加权平均数的公式计算即可; (3)利用样本估计总体的思想,用总数乘以捐款平均数即可得到捐款总数. 【解析】 (1)数据15元出现了20次,出现次数最多,所以众数是15元; ...查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
(本题满分8分)一张长为30cm,宽20cm的矩形纸片,如图1所示,将这张纸片的四个角各剪去一个边长相同的正方形后,把剩余部分折成一个无盖的长方体纸盒,如图1所示,如果折成的长方体纸盒的底面积为264cm2,求剪掉的正方形纸片的边长.
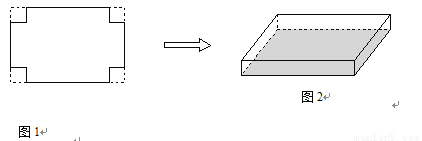
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
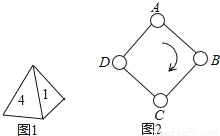
如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4.如图2,正方形ABCD顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.
如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D;若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B;…
设游戏者从圈A起跳.
(1)嘉嘉随机掷一次骰子,求落回到圈A的概率P1;
(2)淇淇随机掷两次骰子,用列表法求最后落回到圈A的概率P2,并指出她与嘉嘉落回到圈A的可能性一样吗?
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在四边形ABCD中,AD、BD相交于点F,点E在BD上,且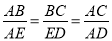 .
.
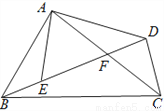
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)判断△ABE与△ACD是否相似?并说明理由.
(1)∠BAE与∠CAD相等(2)△ABE与△ACD相似 【解析】试题分析:(1)、根据,得出△ABC∽△AED,从而说明∠BAC=∠EAD,然后得出答案;(2)、根据得出,结合∠BAE=∠CAD得出三角形相似. 试题解析:(1)∠BAE与∠CAD相等. 在△ABC和△AED中, ∵, ∴△ABC∽△AED, ∴∠BAC=∠EAD, ∴∠BAE=∠CAD;...查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
(本题满分10分)如图,某大楼的顶部竖有一块广告牌CD,小明在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度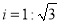 ,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米.(测角器的高度忽略不计,结果精确到0.1米.参考数据: 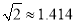 ,
, 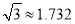 )
)
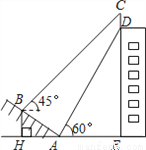
(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(1)5;(2)2.7米 【解析】试题分析:(1)在Rt△ABF中,先由坡度,可求出∠BAH=30°,从而根据30°角的性质求出BH的长; (2)在Rt△ABF中,由勾股定理求出AH的长,从而可求出BG的长度;在Rt△BGC中,可求出CG=BG=5+15;在Rt△ADE中,求出DE=15;最后根据CD=CG+GE﹣DE求解即可. 【解析】 (1)Rt△ABF中, i=ta...查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
(本题满分10分)小明在一次高尔夫球的练习中,在点O处击球,其飞行路线满足抛物线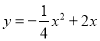 ,其中y(m)是球的飞行高度,
,其中y(m)是球的飞行高度, 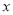 (m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
(m)是球飞出的水平距离,结果球离球洞的水平距离还有2m.
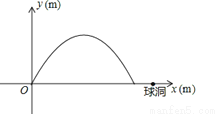
(1)求抛物线的顶点坐标及球飞行的最大水平距离;
(2)若小明第二次仍从点O处击球,球飞行的最大高度不变且刚好进洞,求球飞行的抛物线路线满足的函数表达式.
(1)8m;(2)或 【解析】试题分析:(1)将抛物线配方化顶点式,可求出顶点坐标;令y=0,解方程可求出球飞行的组大水平距离. (2)根据飞行高度不变可得抛物线的顶点坐标,设出顶点式,进而把原点坐标代入即可求得相应的解析式. 【解析】 (1)∵=-, ∴抛物线顶点坐标为(4,4). 解得:x1=0,x2=8, ∴球飞行的最大水平距离为8m. (2)∵最...查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
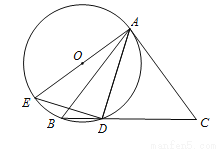
如图,△ABC中,AB=AC,点D为BC上一点,且AD=DC,过A,B,D三点作⊙O,AE是⊙O的直径,连结DE.
(1)求证:AC是⊙O的切线;
(2)若sinC= ,AC=6,求⊙O的直径.
,AC=6,求⊙O的直径.
查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
问题提出
某商店经销《超能陆战队》超萌“小白”(图1)玩具,“小白”玩具每个进价60元.为进行促销,商店制定如下“优惠”方案:如果一次销售数量不超过10个,则销售单价为100元/个;如果一次销售数量超过10个,每增加一个,所有“小白”玩具销售单价降低1元/个,但单价不得低于80元/个.一次销售“小白”玩具的单价y(元/个)与销售数量x(个)之间的函数关系如图2所示.
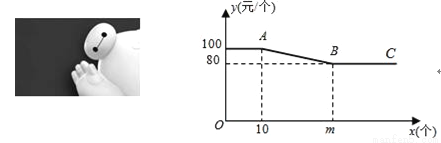
(1)求m的值并解释射线BC所表示的实际意义;
(2)写出该店当一次销售x个时,所获利润w(元)与x(个)之间的函数关系式;
(3)店长经过一段时间的销售发现:即并不是销量越大利润越大(比如,卖25个赚的钱反而比卖30个赚的钱多).为了不出现这种现象,在其他条件不变的情况下,店长应把原来的最低单价80(元/个)至少提高到多少元/个?
(1)m=30,当一次销售数量超过30个以后,都是按单价80元/个销售; (2)当0<x≤10时,w=40x; 当10<x≤30时,w=﹣x2+50x; 当x>30时,w=20x; (3)店家应把最低价每个80元至少提高到每个85元. 【解析】 试题分析:(1)利用价格变化规律,进而求出m的值,然后根据解析式解释线段AB所表示的实际优惠销售政策即可; (2...查看答案和解析>>
科目: 来源:江苏省扬州市2018届九年级上学期期末考试数学试卷 题型:解答题
(本题满分12分)如图,Rt△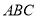 中,
中, 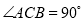 ,
, 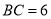 ,点
,点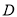 为斜边
为斜边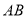 的中点,点
的中点,点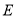 为边
为边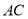 上的一个动点.连结
上的一个动点.连结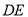 ,过点
,过点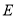 作
作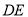 的垂线与边
的垂线与边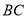 交于点
交于点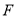 ,以
,以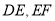 为邻边作矩形
为邻边作矩形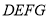 .
.
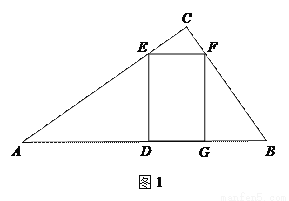
(1)如图1,当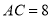 ,点
,点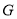 在边
在边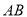 上时,求DE和EF的长;
上时,求DE和EF的长;
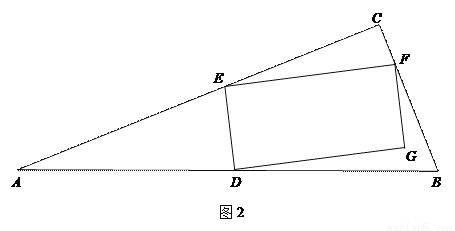
(2)如图2,若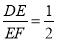 ,设
,设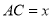 ,矩形
,矩形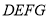 的面积为
的面积为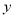 ,求y关于
,求y关于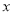 的函数表达式;
的函数表达式;
(3)若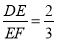 ,且点
,且点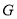 恰好落在Rt△
恰好落在Rt△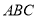 的边上,求
的边上,求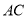 的长.
的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com