
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
将分式方程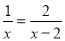 去分母后得到的整式方程正确的是( )
去分母后得到的整式方程正确的是( )
A. x-2=2x B. x2-2x=2x
C. x-2=x D. x=2x-4
A 【解析】方程两边同时乘以x(x-2)得 x-2=2x, 故选A.查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
分式方程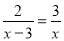 的解为( )
的解为( )
A. x=0 B. x=3
C. x=5 D. x=9
D 【解析】试题分析:方程两边同乘以x(x-3)可得2x=3(x-3),解得x=9,经检验x=9是分式方程的解,故答案选D.查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:解答题
解方程: 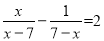 .
.
查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:填空题
小明解方程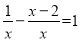 的过程如下,他的解答过程中从第________步开始出现错误.
的过程如下,他的解答过程中从第________步开始出现错误.
【解析】
去分母,得1-(x-2)=1.①
去括号,得1-x+2=1.②
合并同类项,得-x+3=1.③
移项,得-x=-2.④
系数化为1,得x=2.⑤
① 【解析】方程两边同乘x,得:1-(x-2)=x, 所以他的解答过程中从第①步开始出现错误, 故答案为:①.查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
若关于x的方程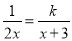 无解,则k的值为( )
无解,则k的值为( )
A. 0或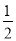 B. -1 C. -2 D. -3
B. -1 C. -2 D. -3
查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:单选题
电动车每小时比自行车多行驶了25千米,自行车行驶30千米比电动车行驶40千米多用了1小时,求两车的平均速度各为多少?设自行车的平均速度为x千米/小时,应列方程为( )
A. 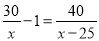 B.
B. 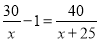
C. 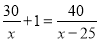 D.
D. 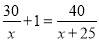
查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:填空题
对于非零实数a,b,规定a?b=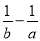 .若2?(2x-1)=1,则x的值为________.
.若2?(2x-1)=1,则x的值为________.
查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:解答题
解分式方程: 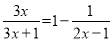 .
.
查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:解答题
某校为了丰富学生的课外体育活动,购买了排球和跳绳,已知排球的单价是跳绳的单价的3倍,购买跳绳共花费了750元,购买排球共花费900元,购买跳绳的数量比购买排球的数量多30个,求跳绳的单价.
15元 【解析】试题分析:首先设跳绳的单价为x元,则排球的单价为3x元,根据题意可得等量关系:750元购进的跳绳个数﹣900元购进的排球个数=30,依此列出方程,再解方程可得答案. 试题解析:【解析】 设跳绳的单价为x元,则排球的单价为3x元,依题意得: ,解方程,得x=15. 经检验:x=15是原方程的根,且符合题意. 答:跳绳的单价是15元.查看答案和解析>>
科目: 来源:2018届中考数学一轮复习单元检测:第6讲 分式方程及其应用 题型:解答题
嘉嘉和琪琪在争论这样一个问题:
嘉嘉说:“分式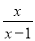 比
比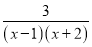 的值多1时,x的值是1.”
的值多1时,x的值是1.”
琪琪说:“分式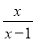 比
比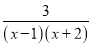 的值多1的情况根本不存在.”
的值多1的情况根本不存在.”
你同意谁的观点呢?请说明理由.
同意琪琪的观点,理由见解析. 【解析】试题分析:解分式方程-1=后即可作出判断. 试题解析:同意琪琪的观点, 理由:由分式比的值多1,可得方程-1=, 去分母,得x(x+2)-(x-1)(x+2)=3, 解得x=1, 经检验,x=1是原分式方程的增根, ∴原分式方程无解,即不存在分式比的值多1的情况.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com