
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:填空题
如果关于x的方程x2﹣2x+k=0(k为常数)有两个不相等的实数根,那么k的取值范围是 .
k<1 【解析】 试题分析:根据一元二次方程ax2+bx+c=0(a≠0)的根的判别式的意义,根据关于x的方程x2﹣2x+k=0(k为常数)有两个不相等的实数根,得到△=>0,即(﹣2)2﹣4×1×k>0,然后解不等式即可求得k<1.查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在△ABC中∠ABC=90°,,AB=4 cm, BC=3cm,动点P以3cm/s的速度由A向C运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交AB于D,则当运动时间为____s时,△ADP是以AP为腰的等腰三角形.
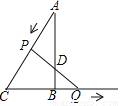
查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:填空题
如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F、G分别在边AB、AD上.则sin∠EFG的值为________.
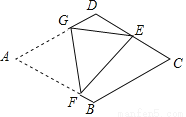
查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
计算:
(1)(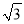 )2-|-6|+(-2)0; (2) (2x+1)(2x-1)-4(x+1)2.
)2-|-6|+(-2)0; (2) (2x+1)(2x-1)-4(x+1)2.
查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
(1)解不等式:2+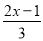 ≤x ; (2)解方程:x2-4x-1=0;
≤x ; (2)解方程:x2-4x-1=0;
查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,在?ABCD中,点E,F在AC上,且∠ABE=∠CDF,求证:BE=DF.
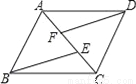
查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
网瘾低龄化问题已经引起社会各界的高度关注,有关部门在全国范围内对12﹣35岁的网瘾人群进行了简单的随机抽样调查,绘制出以下两幅统计图.
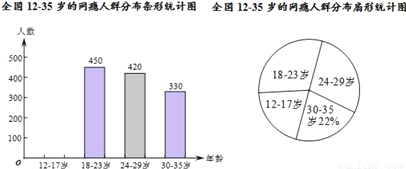
请根据图中的信息,回答下列问题:
(1)这次抽样调查中共调查了 人;
(2)请补全条形统计图;
(3)扇形统计图中18﹣23岁部分的圆心角的度数是 ;
(4)据报道,目前我国12﹣35岁网瘾人数约为2000万,请估计其中12﹣23岁的人数
(1)a=300;(2)108°;(3)12~23岁的人数为400万 【解析】试题分析:(1)根据30-35岁的人数和所占的百分比求调查的人数; (2)从调查的总人数中减去已知的三组的人数,即可得到12-17岁的人数,据此补全条形统计图; (3)先计算18-23岁的人数占调查总人数的百分比,再计算这一组所对应的圆心角的度数; (4)先计算调查中12﹣23岁的人数所占的百分比...查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
如图,甲转盘被分成3个面积相等的扇形,乙转盘被分成4个面积相等的扇形,每一个扇形都标有相应的数字.同时转动两个转盘,当转盘停止后,设甲转盘中指针所指区域内的数字为x,乙转盘中指针所指区域内的数字为y(当指针指在边界线上时,重转一次,直到指针指向一个区域为止).
(1)请你用画树状图或列表格的方法,列出所有等可能情况,并求出点(x,y)落在坐标轴上的概率;
(2)直接写出点(x,y)落在以坐标原点为圆心,2为半径的圆内的概率为_________.
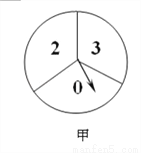
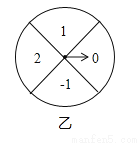
查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
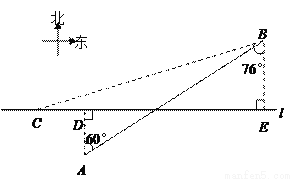
如图,在航线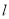 的两侧分别有观测点A和B,点A到航线
的两侧分别有观测点A和B,点A到航线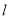 的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
的距离为2km,点B位于点A北偏东60°方向且与A相距10km处.现有一艘轮船从位于点B南偏西76°方向的C处,正沿该航线自西向东航行,5min后该轮船行至点A的正北方向的D处.
(1)求观测点B到航线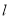 的距离;
的距离;
(2)求该轮船航行的速度(结果精确到0.1km/h).(参考数据: 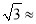 1.73,sin76°≈0.97,cos≈0.24,tan76°≈0.4.01)
1.73,sin76°≈0.97,cos≈0.24,tan76°≈0.4.01)
查看答案和解析>>
科目: 来源:江苏省无锡市2018届九年级上学期期末考试数学试卷 题型:解答题
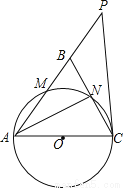
如图,在△ABC中,AB=AC,以AC为直径的⊙O分别交AB、BC于点M、N,直线CP是⊙O的切线,且点P在AB的延长线上.
(1)若∠P=40°,求∠BCP的度数;
(2)若BC=2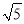 ,sin∠BCP=
,sin∠BCP=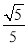 ,求点B到AC的距离.
,求点B到AC的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com