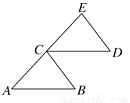
如图，点C是AE的中点，∠A＝∠ECD，AB＝CD，求证：∠B＝∠D．

证明见解析． 【解析】试题分析：由点C是AE的中点，可得AC＝CE，根据已知条件利用SAS判定△ABC≌△CDE，根据全等三角形的性质即可证得结论. 试题解析： 证明：∵点C是AE的中点， ∴AC＝CE. 在△ABC和△CDE中， AC＝CE，∠A＝∠ECD，AB=CD， ∴△ABC≌△CDE(SAS)， ∴∠B＝∠D.

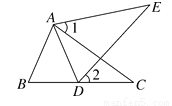
如图，点D在BC上，∠1＝∠2，AE＝AC，下面有三个条件：①AB＝AD；②BC＝DE；③∠E＝∠C，请你从所给条件①②③中选一个条件，使△ABC≌△ADE，并说明理由．

选择②． 【解析】试题分析：由题中给出的条件，可知∠E=∠C，AE=AC，则加入的条件可以是任意一个角或者已知相等角的夹边，所以应选择条件②. 试题解析：因为∠1=∠2，所以∠E=∠ C. 在△ABC和△ADE中， ， 所以△ABC ≌△ADE (SAS). 综上所述，应选择条件②.

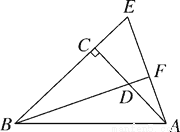
如图，已知Rt△ABC中，∠ACB＝90°，CA＝CB，D是AC上一点，E在BC的延长线上，且AE＝BD，BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系，并说明你猜想的正确性．

猜想：BF⊥AE.理由见解析. 【解析】试题分析：猜想：BF⊥AE 先证明△BDC≌△AEC得出∠CBD=∠CAE，从而得出∠BFE=90°，即BF⊥AE． 【解析】 猜想：BF⊥AE． 理由：∵∠ACB=90°， ∴∠ACE=∠BCD=90°． 又BC=AC，BD=AE， ∴△BDC≌△AEC（HL）． ∴∠CBD=∠CAE． 又∴∠CAE...

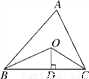
如图，在△ABC中，点O是∠ABC、∠ACB平分线的交点，AB＋BC＋AC＝12，过O作OD⊥BC于D点，且OD＝2，求△ABC的面积．

12 【解析】试题分析：过点O作OE⊥AB于E，OF⊥AC于F，连接OA.根据角平分线的性质得：OE＝OF＝OD＝2.然后根据三角形的面积公式进行计算即可. 试题解析：如图，过点O作OE⊥AB于E，OF⊥AC于F，连接OA. ∵点O是∠ABC，∠ACB平分线的交点， ∴OE＝OD，OF＝OD，即OE＝OF＝OD＝2. ∴S△ABC＝S△ABO＋S△BCO＋S△ACO＝...

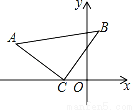
如图，在△ACB中，∠ACB=90°，AC=BC，点C的坐标为（﹣2，0），点A的坐标为（﹣6，3），求点B的坐标．

（1，4）. 【解析】试题分析：过A和B分别作AD⊥OC于D，BE⊥OC于E，利用已知条件可证明△ADC≌△CEB，再由全等三角形的性质和已知数据即可求出B点的坐标． 试题解析：【解析】 过A和B分别作AD⊥OC于D，BE⊥OC于E，∵∠ACB=90°，∴∠ACD+∠CAD=90°∠ACD+∠BCE=90°，∴∠CAD=∠BCE，在△ADC和△CEB中，∵∠ADC=∠CBE=90°，...

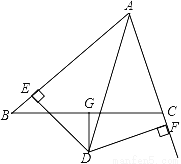
如图，△ABC中，AD平分∠BAC，DG⊥BC且平分BC，DE⊥AB于E，DF⊥AC于F．

（1）求证：BE=CF；

（2）如果AB=8，AC=6，求AE、BE的长．

（1）证明见解析；（2）AE=7，BE=1． 【解析】试题分析：（1）连接DB、DC，先由角平分线的性质就可以得出DE=DF，再证明△DBE≌△DCF就可以得出结论； （2）由条件可以得出△ADE≌△ADF就可以得出AE=AF，进而就可以求出结论． 试题解析：（1）证明：连接DB、DC， ∵DG⊥BC且平分BC， ∴DB=DC． ∵AD为∠BAC的平分线，DE⊥...

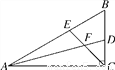
在直角△ABC中，∠ACB＝90°，∠B＝60°，AD，CE分别是∠BAC和∠BCA的平分线，AD，CE相交于点F.

(1)求∠EFD的度数；

(2)判断FE与FD之间的数量关系，并证明你的结论．

（1）120°；（2）FE＝FD. 见解析 【解析】试题分析：（1）根据三角形内角和定理和角平分线的定义计算求解； （2）在AC上截取AG=AE，则EF=FG；根据ASA证明△FGC≌△FDC，得DF=FG，故判断EF=FD． 试题解析：(1)∵△ABC中，∠ACB＝90°，∠B＝60°， ∴∠BAC＝30°. ∵AD，CE分别是∠BAC和∠BCA的平分线， ∴∠F...

下列调查中最适合采用全面调查的是（ ）

A．调查某批次汽车的抗撞击能力

B．端午节期间，抚顺市食品安全检查部门调查市场上粽子的质量情况

C．调查某班40名同学的视力情况

D．调查某池塘中现有鱼的数量

C． 【解析】 试题分析：A．调查某批次汽车的抗撞击能力，破坏力强，适宜抽查； B．端午节期间，抚顺市食品安全检查部门调查市场上粽子的质量情况，范围比较广，适宜抽查； C．调查某班40名同学的视力情况，调查范围比较小，适宜全面调查； D．调查某池塘中现有鱼的数量，调查难度大，适宜抽查． 故选C．

某校学生来自甲、乙、丙三个地区，其人数比为2∶3∶5，如图所示的扇形图表示上述分布情况．已知来自甲地区的为180人，则下列说法不正确的是 (　　)

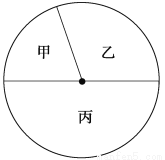
A．扇形甲的圆心角是72°

B．学生的总人数是900人

C．丙地区的人数比乙地区的人数多180人

D．甲地区的人数比丙地区的人数少180人

D 【解析】由已知得，扇形甲的圆心角是×360°＝72°，A选项正确；学生的总人数是180÷＝900，B选项正确；乙地区的人数900×＝270，丙地区的人数是900×＝450，所以C选项正确，故选D.

甲校女生占全校总人数的50％，乙校男生占全校总人数的50％，比较两校女生人数（ ）

A. 甲校女生人数多 B. 乙校女生人数多

C. 甲校与乙校女生人数一样多 D. 以上说法都不对

D 【解析】试题分析：由题可知甲乙两校女生均占本校总人数的50％，但是两校总人数都是未知的所以无法比较两校女生人数，故选D.