
科目: 来源:北师大版七年级下册数学 第五章 生活中的轴对称 单元检测卷 题型:解答题
(本题6分) 如图,在11×11的正方形网格中,网格中有一个格点△ABC(即三角形的顶点都在格点上).
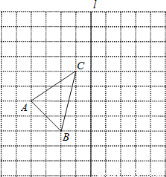
(1)在图中作出△ABC关于直线l对称的△A1B1C1 (要求A与A1,B与B1,C与C1相对应) ;
(2)在直线l上找一点P,使得△PAC的周长最小.
【解析】 试题分析:(1)根据网格结构找出点A、B、C 关于直线l的对称点A1、B1、C1的位置,然后顺次连接即可; (2)有题意知只要让PA+PC最短即可,也就是根据对称的性质,C′A与l的交点即为P点,因此这时候的. △PAC的周长最小.查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
等腰三角形的一腰长为6cm, 底边长为6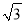 cm, 则其底角为()
cm, 则其底角为()
A. 30° B. 60° C. 90° D. 120°
A 【解析】【解析】 如图,作AD⊥BC于D点,则BD=DC=.∵AC=6,∴cos∠C=,∴∠C=30°.故选A.查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
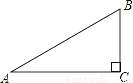
如图,在Rt△ABC中,∠C=Rt∠,则cosA可表示为( )
A. 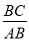 B.
B. 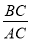 C.
C. 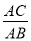 D.
D. 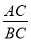
查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
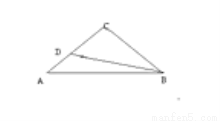
如图:在等腰△ABC中,∠C=90º,AC=6,D 是AC上一点,若tan∠DBA=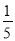 ,则A D的长为( )
,则A D的长为( )
A. 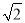 B. 2 C. 1 D. 2
B. 2 C. 1 D. 2
查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
如图,在平面直角坐标系中,直线OA过点(2,1),则tanα的值是( )
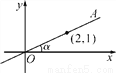
A. 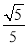 B.
B. 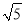 C.
C. 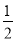 D. 2
D. 2
查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
把△ABC三边的长度都扩大为原来的3倍,则锐角A的正弦函数值( )
A. 不变 B. 缩小为原来的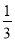 C. 扩大为原来的3倍 D. 不能确定
C. 扩大为原来的3倍 D. 不能确定
查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
如图,P是∠α的边OA上一点,且点P的坐标为(4,3),则cosα等于( )
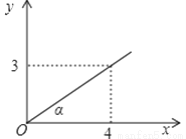
A. 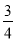 B.
B. 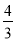 C.
C. 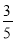 D.
D. 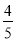
查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
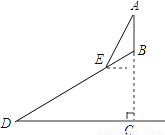
某山的山顶B处有一个观光塔,已知该山的山坡面与水平面的夹角∠BDC为30°,山高BC为100米,点E距山脚D处150米,在点E处测得观光塔顶端A的仰角为60°,则观光塔AB的高度是( )
A. 50米 B. 100米 C. 125米 D. 150米
A 【解析】试题解析:作EF⊥AC于F,EG⊥DC于G, 在Rt△DEG中,EG=DE=75米, ∴BF=BC-CF=BC-CE=100-75=25(米), EF==25, ∵∠AEF=60°, ∴∠A=30°, ∴AF==75(米), ∴AB=AF-BF=50(米), 故观光塔AB的高度为50米. 故选A.查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
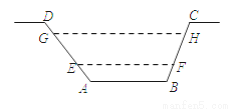
如图,某水渠的横断面是等腰梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是( )米.
A. 1.2 B. 1.1 C. 0.8 D. 2.2
B 【解析】【解析】 过点E作EM⊥GH于点M,过点F作FN⊥GH于点N,可得四边形EFNM为矩形,则MN=EF,设ME=FN=x,在Rt△GME中,∵斜坡AD的坡度为1:1.2,∴ME:GM=1:1.2,∴GM=1.2x.在Rt△NHF中,∵斜坡BC的坡度为1:0.8,∴NF:NH=1:0.8,∴NH=0.8x,则GH=1.2x+0.8x+3.8=6,解得:x=1.1.故选B.查看答案和解析>>
科目: 来源:北师大版九年级下册数学第一章直角三角形的边角关系单元检测卷 题型:单选题
在Rt△ABC中,cotA=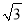 , 则∠A的度数是( )
, 则∠A的度数是( )
A. 90° B. 60° C. 45° D. 30°
D 【解析】试题分析:在Rt△ABC中,cotA=,所以∠A=300. 故选D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com