
科目: 来源:人教版九年级下册数学全册综合测试一 题型:解答题
已知函数y=(m﹣1)x|m|﹣2是反比例函数.
(1)求m的值;
(2)求当x=3时,y的值.
(1)m=﹣1 (2)﹣ 【解析】 试题分析:(1)让x的次数等于﹣1,系数不为0列式求值即可; (2)把x=3代入(1)中所得函数,求值即可. 【解析】 (1)|m|﹣2=﹣1且m﹣1≠0, 解得:m=±1且m≠1, ∴m=﹣1. (2)当m=﹣1时,原方程变为y=﹣, 当x=3时,y=﹣.查看答案和解析>>
科目: 来源:人教版九年级下册数学全册综合测试一 题型:解答题
如图,抛物线y= 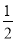 x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
x2+bx﹣2与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0).
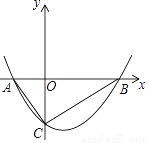
(1)求抛物线的解析式;
(2)判断△ABC的形状,证明你的结论.
(1)y= x2﹣ x﹣2;(2)见解析 【解析】试题分析:(1)因为点A在抛物线上,所以将点A代入函数解析式即可求得; (2)由函数解析式可以求得其与x轴、y轴的交点坐标,即可求得AB、BC、AC的长,由勾股定理的逆定理可得三角形的形状. 试题解析:(1)∵点A(-1,0)在抛物线y=x2+bx-2上, ∴×(-1)2+b×(-1)-2=0,b=- ∴抛物线的解析式...查看答案和解析>>
科目: 来源:人教版九年级下册数学全册综合测试一 题型:解答题
如图1,P为∠MON平分线OC上一点,以P为顶点的∠APB两边分别与射线OM和ON交于A、B两点,如果∠APB在绕点P旋转时始终满足OA•OB=OP2 , 我们就把∠APB叫做∠MON的关联角.
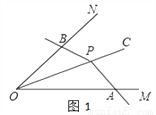
(1)如图2,P为∠MON平分线OC上一点,过P作PB⊥ON于B,AP⊥OC于P,那么∠APB________∠MON的关联角(填“是”或“不是”).
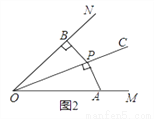
(2)①如图3,如果∠MON=60°,OP=2,∠APB是∠MON的关联角,连接AB,求△AOB的面积和∠APB的度数;
②如果∠MON=α°(0°<α°<90°),OP=m,∠APB是∠MON的关联角,直接用含有α和m的代数式表示△AOB的面积.
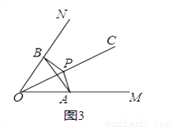
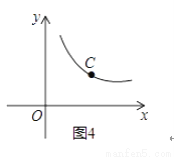
(3)如图4,点C是函数y=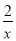 (x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
(x>0)图象上一个动点,过点C的直线CD分别交x轴和y轴于A,B两点,且满足BC=2CA,直接写出∠AOB的关联角∠APB的顶点P的坐标.
查看答案和解析>>
科目: 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:单选题
如图,在Rt△ABC中,∠C=90°,∠B=30°,AB=8,则BC的长是( )
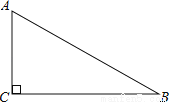
A. 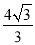 B. 4 C.
B. 4 C. 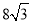 D.
D. 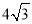
查看答案和解析>>
科目: 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:单选题
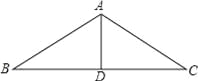
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )
A. 5sin36°米 B. 5cos36°米 C. 5tan36°米 D. 10tan36°米
C 【解析】试题分析:∵AB=AC,AD⊥BC,BC=10米,∴DC=BD=5米,在Rt△ADC中,∠B=36°,∴tan36°=,即AD=BD•tan36°=5tan36°(米).故选C.查看答案和解析>>
科目: 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:单选题
一座楼梯的示意图如图所示,BC是铅垂线,CA是水平线,BA与CA的夹角为θ.现要在楼梯上铺一条地毯,已知CA=4米,楼梯宽度为1米,则地毯的面积至少需要( )
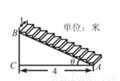
A. 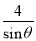 米² B.
米² B. 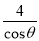 米² C. (
米² C. (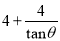 )米² D. (
)米² D. (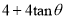 )米²
)米²
查看答案和解析>>
科目: 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:填空题
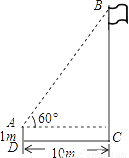
如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为________ m(结果保留根号).
查看答案和解析>>
科目: 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:填空题
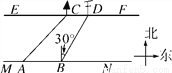
在综合实践课上,小聪所在小组要测量一条河的宽度,如图,河岸EF∥MN,小聪在河岸MN上点A处用测倾器测得河对岸小树C位于东北方向,然后沿河岸走了30米,到达B处,测得河对岸电线杆D位于北偏东30°方向,此时,其他同学测得CD=10米.则河的宽度为________米(结果保留根号).
查看答案和解析>>
科目: 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:填空题
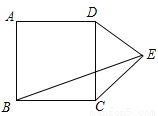
如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC= .
查看答案和解析>>
科目: 来源:2018届中考数学专题复习同步练习题:锐角三角函数和解直角三角形(有答案) 题型:解答题
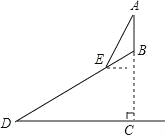
某班数学兴趣小组利用数学活动课时间测量位于烈山山顶的炎帝雕像高度,已知烈山坡面与水平面的夹角为30°,山高857.5尺,组员从山脚D处沿山坡向着雕像方向前进1620尺到达E点,在点E处测得雕像顶端A的仰角为60°,求雕像AB的高度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com