
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:单选题
已知△ABC∽△A′B′C′,△A′B′C′的面积为6cm2,周长为△ABC周长的一半,则△ABC的面积等于( )
A. 1.5cm2 B. 3cm2 C. 12cm2 D. 24cm2
D 【解析】根据题意求出两个三角形的周长比,即可得出相似比,然后根据相似三角形的性质解答即可. 【解析】 ∵△ABC与△A′B′C′的周长比为2:1,且△ABC∽△A′B′C′, ∴△ABC与△A′B′C′的面积比为4:1,又△A′B′C′的面积为6 cm2, ∴△ABC的面积=24 cm2, 故选:D.查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
已知x=1是方程x2-4x+c=0的一个根,则c的值是_________.
3 【解析】试题分析:把x=2代入x2-4x+c=0,得22-4×2+c=0, 解得c=4.查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
如图,已知直线l1∥l2∥l3,分别交直线m,n于点A,D,B,E,C,F,AB=5cm,AC=15cm,DE=3cm,则EF的长为________cm.
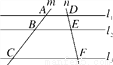
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
一个不透明的袋子中有1个白球、3个黄球和2个红球,这些球除颜色外都相同.将袋子中的球搅拌均匀,从中一次随机摸出两个球都是黄球的概率为_______.
【解析】试题分析:画树形图得: 所以两次都摸到白球的概率==.故答案为.查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
将一副三角尺按如图所示的方式叠放在一起,边AD与BC相交于点E,则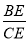 的值等于_________.
的值等于_________.
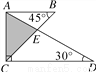
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
如图所示是反比例函数y=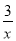 与y=-
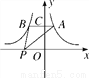
与y=-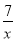 在x轴上方的图象,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上运动,则△ABP的面积等于________.
在x轴上方的图象,点C是y轴正半轴上的一点,过点C作AB∥x轴分别交这两个图象于点A,B.若点P在x轴上运动,则△ABP的面积等于________.
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:填空题
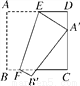
如图,正方形纸片ABCD的边长为12,E,F分别是边AD,BC上的点,将正方形纸片沿EF折叠,使得点A落在CD边上的点A′处,此时点B落在点B′处.已知折痕EF=13,则AE的长等于_________.
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:解答题
解方程:x2+2x-1=0.
x1=-1+,x2=-1-. 【解析】利用公式法即可求解. 【解析】 ∵a=1,b=2,c=-1, ∴b2-4ac=22-4×1×(-1)=8, ∴x=, 即x1=-1+,x2=-1-.查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:解答题
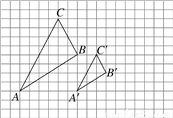
如图,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在正方形网格的格点上.
(1)画出位似中心O;
(2)△ABC与△A′B′C′的相似比为__________,面积比为__________.
查看答案和解析>>
科目: 来源:2017-2018学年九年级数学北师大版上册 全册综合测试卷2 题型:解答题
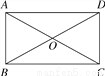
如图,在?ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=4,求BC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com