
科目: 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:解答题
用一水管向某容器内持续注水,设单位时间内注入的水量保持不变;在注水过程中,表示容器内水深h与注水时间t的关系有如图所示的A,B,C,D四个图象,它们分别与E,F,G,H四种容器中的其中一种相对应,请你把相对应容器的字母填在下面的横线上.
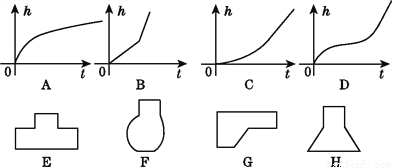
A→____________;B→____________;C→____________; D→____________.
G E H F 【解析】试题分析:先根据函数的四个图象分析其变化,再找出相应的容器即可. 试题解析:A、由函数的图象可知,当向容器中注水时,水面先急剧升高,再缓慢升高,所以对应的容器应是底部较窄,缓慢变宽,故应对应G; B、由函数的图象可知,当向容器中注水时,一开始一段容器应较宽,且时直面,后一段较窄,也是直面,故应对应E; C、函数图象先缓慢上升,再急剧上升,故应对应H;...查看答案和解析>>
科目: 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )
A. 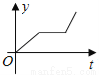 B.
B. 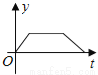 C.
C. 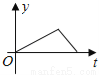 D.
D. 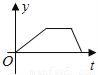
查看答案和解析>>
科目: 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
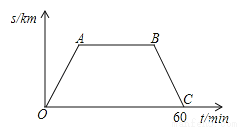
星期六早晨蕊蕊妈妈从家里出发去观山湖公园锻炼,她连续、匀速走了60min后回家,图中的折线段OA﹣AB﹣BC是她出发后所在位置离家的距离s(km)与行走时间t(min)之间的函数关系,则下列图形中可以大致描述蕊蕊妈妈行走的路线是( )
A.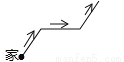 B.
B.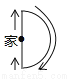 C.
C. D.
D.
查看答案和解析>>
科目: 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
如图所示的折线图描述了某地某日的气温变化情况.
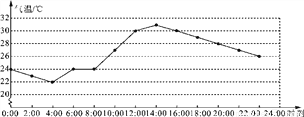
根据图中信息,下列说法错误的是( )
A. 4:00气温最低 B. 6:00气温为24 ℃
C. 14:00气温最高 D. 气温是30 ℃的时刻为16:00
D 【解析】试题分析:根据观察函数图象的横坐标,可得时间,根据观察函数图象的纵坐标,可得气温. 【解析】 A、由横坐标看出4:00气温最低是24℃,故A正确; B、由纵坐标看出6:00气温为24℃,故B正确; C、由横坐标看出14:00气温最高31℃; D、由横坐标看出气温是30℃的时刻是12:00,16:00,故D错误; 故选:D.查看答案和解析>>
科目: 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
如图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
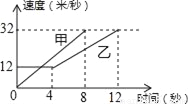
A. 乙前4秒行驶的路程为48米
B. 在0到8秒内甲的速度每秒增加4米/秒
C. 两车到第3秒时行驶的路程相等
D. 在4至8秒内甲的速度都大于乙的速度
C 【解析】试题分析:A.根据图象可得,乙前4秒行驶的路程为12×4=48米,正确; B.根据图象得:在0到8秒内甲的速度每秒增加4米秒/,正确; C.根据图象可得两车到第3秒时行驶的路程不相等,故本选项错误; D.在4至8秒内甲的速度都大于乙的速度,正确; 故选C.查看答案和解析>>
科目: 来源:北师大版七年级数学下3.3 用图象表示的变量间关系 同步练习 题型:单选题
如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm)在下列图象中,表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
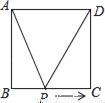
A. 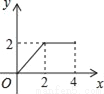 B.
B. 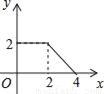 C.
C. 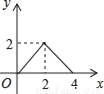 D.
D. 
查看答案和解析>>
科目: 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:单选题
如图,a,b,c分别表示△ABC的三边长,则下面与△ABC一定全等的三角形是( )
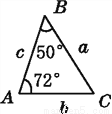
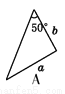
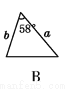
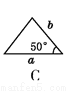
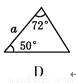
查看答案和解析>>
科目: 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:单选题
如图,在△ABC和△DEF中,∠B=∠DEF,AB=DE,添加下列一个条件后,仍然不能证明△ABC≌△DEF,这个条件是( )
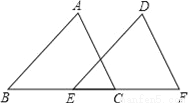
A. ∠A=∠D B. BC=EF C. ∠ACB=∠F D. AC=DF
D 【解析】【解析】 ∵∠B=∠DEF,AB=DE,∴添加∠A=∠D,利用ASA可得△ABC≌△DEF; ∴添加BC=EF,利用SAS可得△ABC≌△DEF; ∴添加∠ACB=∠F,利用AAS可得△ABC≌△DEF; 故选D.查看答案和解析>>
科目: 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:单选题
如图,点E,F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加的一个条件是( )
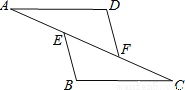
A. ∠A=∠C B. ∠D=∠B C. AD∥BC D. DF∥BE
B 【解析】试题分析:利用全等三角形的判定与性质进而得出当∠D=∠B时,△ADF≌△CBE. 当∠D=∠B时, 在△ADF和△CBE中 ∵, ∴△ADF≌△CBE(SAS)查看答案和解析>>
科目: 来源:北师大版七年级数学下4.3.3 用“边角边”判定三角形全等 同步练习 题型:单选题
如图,已知AB=AE,AC=AD,下列条件中不能判定△ABC≌△AED的是( )
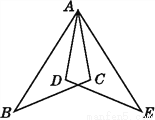
A. BC=ED B. ∠BAD=∠EAC
C. ∠B=∠E D. ∠BAC=∠EAD
C 【解析】解:A.∵AB=AE,AC=AD,BC=ED,∴△ABC≌△AED(SSS),故A不符合题意; B. ∵∠BAD=∠EAC,∴∠BAC=∠EAD.∵AB=AE,∠BAC=∠EAD ,AC=AD, ∴△ABC≌△AED(SAS),故B不符合题意; C.不能判定△ABC≌△AED,故C符合题意. D.∵AB=AE, ∠BAC=∠EAD,AC=AD,∴△ABC≌△AE...查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com