过△ABC的顶点A,作BC边上的高,以下作法正确的是(　　)

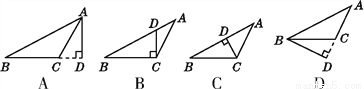
A. A B. B C. C D. D

A 【解析】【解析】 △ABC中BC边上的高正确的是A选项．故选A．

如图，△ABC的面积为16，点D是BC边上一点，且BD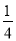＝BC，点G是AB边上一点，点H在△ABC内部，BD∥GH，且BD＝GH.则图中阴影部分的面积是(　　)

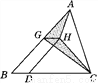
A. 3 B. 4 C. 5 D. 6

B 【解析】试题分析：设△ABC底边BC上的高为h，△AGH底边GH上的高为h1，△CGH底边GH上的高为h2， 则有h=h1+h2．所以S△ABC=BC•h=16，S阴影=S△AGH+S△CGH=GH•h1+GH•h2=GH•（h1+h2）=GH•h．因为四边形BDHG是平行四边形，且BD=BC，可得GH=BD=BC，所以S阴影=×（BC•h）=S△ABC=4． 故答案选B． ...

如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（　　）

A. 锐角三角形 B. 钝角三角形 C. 直角三角形 D. 都有可能

C 【解析】A. 锐角三角形，三条高线交点在三角形内，故错误； B. 钝角三角形，三条高线不会交于一个顶点，故错误； C. 直角三角形的直角所在的顶点正好是三条高线的交点，可以得出这个三角形是直角三角形，故正确； D. 能确定C正确，故D错误。 故选C.

不一定在三角形内部的线段是( )

A. 三角形的角平分线 B. 三角形的中线

C. 三角形的高 D. 以上都不对

C 【解析】试题解析：三角形的角平分线、中线一定在三角形的内部， 直角三角形的高线有两条是三角形的直角边， 钝角三角形的高线有两条在三角形的外部， 所以，不一定在三角形内部的线段是三角形的高. 故选C.

下列说法中正确的是(　　)

A. 三角形的三条高都在三角形内 B. 直角三角形只有一条高

C. 锐角三角形的三条高都在三角形内 D. 三角形每一边上的高都小于其他两边

C 【解析】【解析】 三角形的高不一定在三角形内，故A错误； 任何三角形都有三条高，故B错误； 锐角三角形的三条高都在三角形内，正确； 直角三角形一条直角边的高等于另一条直角边，故D错误． 故选C．

下列结论:①三角形的角平分线、中线、高都是线段;②直角三角形只有一条高;③三角形的中线可能在三角形外部;④三角形的高都在三角形内部.

其中正确的有(　　)

A. 1个 B. 2个 C. 3个 D. 4个

A 【解析】【解析】 ①三角形的角平分线、中线、高都是线段，正确； ②直角三角形有三条高，故②错误； ③三角形的中线可能在三角形外部，错误； ④三角形的高都在三角形内部，错误． 故正确的只有①，故选A．

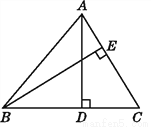
如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,若BC=10,AC=8,BE=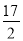,求AD的长.

6.8 【解析】试题分析：根据S△ABC=·BC·AD=·AC·BE即可得出结论． 试题解析：【解析】 因为AD⊥BC，BE⊥AC，所以S△ABC=·BC·AD=·AC·BE．所以BC·AD=AC·BE．又因为BC=10，AC=8，BE=，所以10AD=8×，所以AD=6.8．

已知AD是△ABC的高,∠BAD=72°,∠CAD=21°,求∠BAC的度数.

93°; 51° 【解析】试题分析：分高AD在△ABC内部和外部两种情况讨论求解即可． 试题解析：【解析】 ①如图1，当高AD在△ABC的内部时，∠BAC=∠BAD+∠CAD=72°+21°=93°； ②如图2，当高AD在△ABC的外部时，∠BAC=∠BAD﹣∠CAD=72°﹣21°=51°． 综上所述：∠BAC的度数为93°或51°．故答案为：93°或51°．

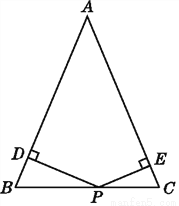
如图,已知在△ABC中,AB=AC=4,P是BC边上任一点,PD⊥AB,PE⊥AC,D,E为垂足.若△ABC的面积为6,问:PD+PE的值能否确定?若能确定,值是多少?请说明理由.

PD+PE的值能确定,且PD+PE=3 【解析】试题分析：可连接AP，由图得，S△ABC=S△ABP+S△ACP，代入数值，求解即可． 试题解析：【解析】 PD+PE的值能确定，且PD+PE=3．理由如下： 如图，连接AP． 由图可得S△ABC=S△ABP+S△ACP． 因为PD⊥AB，PE⊥AC，AB=AC=4，△ABC的面积为6， 所以6=×4×PD+×4...

一个等腰三角形的两边长分别为4，8，则它的周长为（　　）

A. 12 B. 16 C. 20 D. 16或20

C 【解析】试题分析：由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析． ①当4为腰时，4+4=8，故此种情况不存在；②当8为腰时，8﹣4＜8＜8+4，符合题意． 故此三角形的周长=8+8+4=20．