练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    一个等腰三角形的两边长分别为4，8，则它的周长为（　　）

    A. 12 B. 16 C. 20 D. 16或20

    C 【解析】试题分析：由于题中没有指明哪边是底哪边是腰，则应该分两种情况进行分析． ①当4为腰时，4+4=8，故此种情况不存在；②当8为腰时，8﹣4＜8＜8+4，符合题意． 故此三角形的周长=8+8+4=20．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：北师大版七年级下册4.3.2探索三角形全等的条件练习 题型：解答题

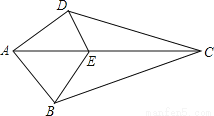
    如图，已知，在四边形ABCD中，E是AC上一点，∠DAC=∠BAC，∠DCA=∠BCA．求证：∠DEC=∠BEC。

    证明见解析 【解析】分析：易证△ACD≌△ACB，可得BC=CD，即可证明△DCE≌△BCE，可得∠DEC=∠BEC，即可解题． 本题解析： 在△ACD和△ACB中， ∴△ACD≌△ACB，（ASA） ∴BC=CD， 在△DCE和△BCE中， ∴△DCE≌△BCE（ASA）， ∴∠DEC=∠BEC。

    查看答案和解析>>

    科目：初中数学 来源：北师大七年级下1.7 整式的除法 同步练习含答案 题型：单选题

    下列各式,计算结果错误的是(　　)

    A. (3a2+2a-6ab)÷2a=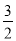a-3b+1

    B. (-4a3+12a2b-7a3b2)÷(-4a2)=a-3b+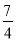ab2

    C. (4xm+2-5xm-1)÷3xm-2=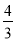x4-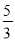

    D. (3an+1+an+2-12an)÷(-24an)=- 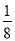a-a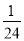2+

    C 【解析】A. ∵ (3a2+2a-6ab)÷2a=a-3b+1，故正确； B. (-4a3+12a2b-7a3b2)÷(-4a2)=a-3b+ab2，故正确； C. (4xm+2-5xm-1)÷3xm-2=x4-x，故不正确； D. (3an+1+an+2-12an)÷(-24an)=- a-a2+，故正确；

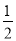
    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    已知三角形的三边长为连续整数，且周长为12cm，则它的最短边长为（　　）

    A. 2cm B. 3cm C. 4cm D. 5cm

    B 【解析】试题解析：设大小处于中间的边长是xcm，则最大的边是(x+1)cm，最小的边长是(x?1)cm. 则(x+1)+x+(x?1)=12， 解得：x=4， 则最短的边长是：4?1=3cm. 故选B.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.2 三角形的三边关系 同步练习 题型：单选题

    三角形按边可分为(　　)

    A. 等腰三角形、直角三角形、锐角三角形

    B. 直角三角形、不等边三角形

    C. 等腰三角形、不等边三角形

    D. 等腰三角形、等边三角形

    C 【解析】由于三角形按边分类可以分为：等腰三角形和不等边三角形两大类. 故选C.

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：单选题

    下列说法中正确的是(　　)

    A. 三角形的三条高都在三角形内 B. 直角三角形只有一条高

    C. 锐角三角形的三条高都在三角形内 D. 三角形每一边上的高都小于其他两边

    C 【解析】【解析】 三角形的高不一定在三角形内，故A错误； 任何三角形都有三条高，故B错误； 锐角三角形的三条高都在三角形内，正确； 直角三角形一条直角边的高等于另一条直角边，故D错误． 故选C．

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级数学下4.1.3 三角形的中线、角平分线 同步练习 题型：解答题

    如图,AD是∠CAB的平分线,DE∥AB,DF∥AC,EF交AD于点O.请问:

    (1)DO是∠EDF的平分线吗?给出结论并说明理由.

    (2)若将DO是∠EDF的平分线与AD是∠CAB的平分线,DE∥AB,DF∥AC中的任一条件交换,所得结论正确吗?若正确,请选择一个说明理由.

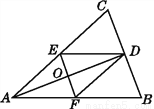
    (1)DO是∠EDF的平分线(2)正确.若和DE∥AB交换. 【解析】试题分析：（1）由角平分线定义得到∠EAD=∠FAD，再由平行线的性质得到∠EDA=∠FAD，∠FDA=∠EAD，从而得到∠EDA=∠FDA，即可得到结论． （2）正确．若和DE∥AB交换．则由平行线的性质得到∠FDA=∠EAD，再由角平分线的定义得到∠EAD=∠FAD，故有∠FAD=∠FDA．由DO是∠EDF的平分...

    查看答案和解析>>

    科目：初中数学 来源：北师大版七年级下册 第四章 三角形 4.5 利用三角形全等测距离 同步测试 题型：解答题

    如图，一艘轮船沿AC方向航行，轮船在点A时测得航线两侧的两个灯塔D、E与航线的夹角相等，当轮船到达点B时测得这两个灯塔与航线的夹角仍然相等，这时轮船与两个灯塔的距离是否相等？为什么？

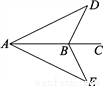
    见解析 【解析】分析：根据轮船在点A时两个灯塔与航线的夹角相等可得∠DAB=∠EAB，轮船到达点B时两个灯塔与航线的夹角仍然相等可得∠1=∠2，再根据等角的补角相等推出∠3=∠4，然后利用角边角定理证明△ABD与△ABE全等，然后根据全等三角形对应边相等即可证明． 本题解析： 到达点B时轮船与两个灯塔的距离相等。 理由如下： 根据题意得，∠DAB=∠EAB，∠1=∠2...

    查看答案和解析>>

    科目：初中数学 来源：江苏省扬州市2017-2018学年八年级上学期期末考试数学试卷 题型：填空题

    已知关于x，y的二元一次方程组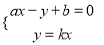（a，b，k均为常数，且a≠0，k≠0）的解为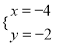，则直线y=ax+b和直线y=kx的交点坐标为________．

    (-4,-2) 【解析】试题解析：因为关于x，y的二元一次方程组（a，b，k均为常数，且a≠0，k≠0）的解为， 则直线y=ax+b和直线y=kx的交点坐标为（-4，-2）， 故答案为：（-4，-2）．

    查看答案和解析>>

    同步练习册答案