
科目: 来源:江苏省东台市第四教育联盟2018届九年级下学期第一次质量检测数学试卷 题型:解答题
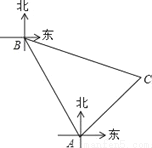
某海域有A、B两个港口,B港口在A港口北偏西30°方向上,距A港口60海里,有一艘船从A港口出发,沿东北方向行驶一段距离后,到达位于B港口南偏东75°方向的C处,求:
(1)∠C= °;
(2)此时刻船与B港口之间的距离CB的长(结果保留根号).
查看答案和解析>>
科目: 来源:江苏省东台市第四教育联盟2018届九年级下学期第一次质量检测数学试卷 题型:解答题
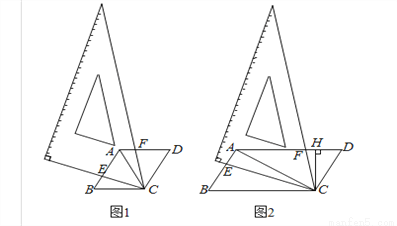
数学活动课上,励志学习小组对有一内角为120°的平行四边形ABCD(∠BAD=120°)进行探究:将一块含60°的直角三角板如图放置在平行四边形ABCD所在平面内旋转,且60°角的顶点始终与点C重合,较短的直角边和斜边所在的两直线分别交线段AB,AD于点E,F(不包括线段的端点).
(1)初步尝试
如图1,若AD=AB,求证:①△BCE≌△ACF,②AE+AF=AC;
(2)类比发现
如图2,若AD=2AB,过点C作CH⊥AD于点H,求证:AE=2FH;
在证明这道题时,励志学习小组成员小颖同学进行如下书写,请你将此证明过程补充完整
证明:设DH=x,由由题意,CD=2x,CH= x,
x,
∴AD=2AB=4x,
∴AH=AD﹣DH=3x,
∵CH⊥AD,
∴AC= =2
=2 x,
x,
(3)深入探究
在(2)的条件下,励志学习小组成员小漫同学探究发现 ,试判断小漫同学的结论是否正确,并说明理由
,试判断小漫同学的结论是否正确,并说明理由
查看答案和解析>>
科目: 来源:江苏省东台市第四教育联盟2018届九年级下学期第一次质量检测数学试卷 题型:解答题
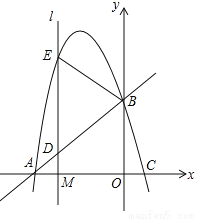
(2017贵州省遵义市)如图,抛物线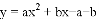 (a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为
(a<0,a、b为常数)与x轴交于A、C两点,与y轴交于B点,直线AB的函数关系式为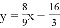 .
.
(1)求该抛物线的函数关系式与C点坐标;
(2)已知点M(m,0)是线段OA上的一个动点,过点M作x轴的垂线l分别与直线AB和抛物线交于D、E两点,当m为何值时,△BDE恰好是以DE为底边的等腰三角形?
(3)在(2)问条件下,当△BDE恰好是以DE为底边的等腰三角形时,动点M相应位置记为点M′,将OM′绕原点O顺时针旋转得到ON(旋转角在0°到90°之间);
①探究:线段OB上是否存在定点P(P不与O、B重合),无论ON如何旋转,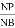 始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
始终保持不变,若存在,试求出P点坐标;若不存在,请说明理由;
②试求出此旋转过程中,(NA+ NB)的最小值.
NB)的最小值.
查看答案和解析>>
科目: 来源:2017-2018学年人教版七年级下册数学综合题型练习卷:平行线与相交线 题型:解答题
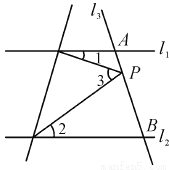
如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).
查看答案和解析>>
科目: 来源:2017-2018学年人教版七年级下册数学综合题型练习卷:平行线与相交线 题型:解答题
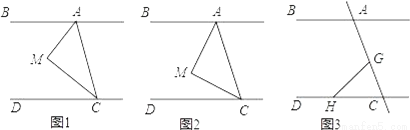
(1)如图1,CM平分∠ACD,AM平分∠BAC,∠MAC+∠ACM=90°,请判断AB与CD的位置关系并说明理由;
(2)如图2,当∠M=90°且AB与CD的位置关系保持(1)中的不变,当直角顶点M移动时,问∠BAM与∠MCD是否存在确定的数量关系?并说明理由;
(3)如图3,G为线段AC上一定点,点H为直线CD上一动点且AB与CD的位置关系保持(1)中的不变,当点H在射线CD上运动时(点C除外)∠CGH+∠CHG与∠BAC有何数量关系?猜想结论并说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年人教版七年级下册数学综合题型练习卷:平行线与相交线 题型:解答题
下列各图中的MA1与NAn平行.
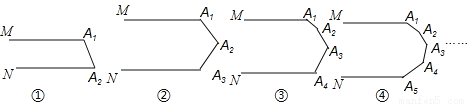
(1)图①中的∠A1+∠A2= 度,图②中的∠A1+∠A2+∠A3= 度,
图③中的∠A1+∠A2+∠A3+∠A4= 度,图④中的∠A1+∠A2+∠A3+∠A4+∠A5= 度,…,
第⑩个图中的∠A1+∠A2+∠A3+…+∠A10= 度
(2)第n个图中的∠A1+∠A2+∠A3+…+∠An= .
查看答案和解析>>
科目: 来源:2017-2018学年人教版七年级下册数学综合题型练习卷:平行线与相交线 题型:解答题
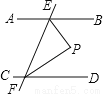
如图,已知AB∥CD,EF与AB、CD分别相交于点E、F,∠BEF与∠EFD的平分线相交于点P,求证:EP⊥FP.
查看答案和解析>>
科目: 来源:2017-2018学年人教版七年级下册数学综合题型练习卷:平行线与相交线 题型:解答题
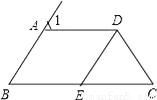
如图,AD∥BC,∠1=∠C,∠B=60°.
(1)求∠C= °;
(2)如果DE是∠ADC的平分线,那么DE与AB平行吗?请说明理由.
查看答案和解析>>
科目: 来源:2017-2018学年人教版七年级下册数学综合题型练习卷:平行线与相交线 题型:解答题
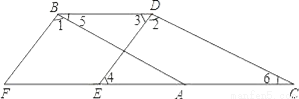
如图,已知∠1=∠2,∠3=∠4,∠5=∠6,试判断ED与FB的位置关系,并说明为什么.
查看答案和解析>>
科目: 来源:2017-2018学年人教版七年级下册数学综合题型练习卷:平行线与相交线 题型:解答题
探索:小明和小亮在研究一个数学问题:已知AB∥CD,AB和CD都不经过点P,探索∠P与∠A,∠C的数量关系.
发现:在图1中,小明和小亮都发现:∠APC=∠A+∠C;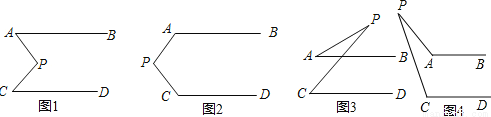
小明是这样证明的:过点P作PQ∥AB
∴∠APQ=∠A( )
∵PQ∥AB,AB∥CD.
∴PQ∥CD( )
∴∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
小亮是这样证明的:过点作PQ∥AB∥CD.
∴∠APQ=∠A,∠CPQ=∠C
∴∠APQ+∠CPQ=∠A+∠C
即∠APC=∠A+∠C
请在上面证明过程的过程的横线上,填写依据;两人的证明过程中,完全正确的是 .
应用:
在图2中,若∠A=120°,∠C=140°,则∠P的度数为 ;
在图3中,若∠A=30°,∠C=70°,则∠P的度数为 ;
拓展:
在图4中,探索∠P与∠A,∠C的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com