阅读材料：如图①，在平面直角坐标系中，A，B两点的坐标分别为A(x1，y1)，B(x2，y2)，AB的中点P的坐标为(xp，yp)．由xp－x1＝x2－xp，得xp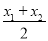＝，同理得yp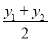＝，所以AB的中点坐标为P(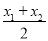,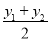).由勾股定理得AB2＝|x2－x1|2＋|y2－y1|2，所以A，B两点间的距离公式为AB＝.

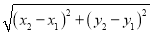注：上述公式对A，B在平面直角坐标系中其他位置也成立．

解答下列问题：

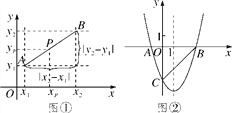
如图②，抛物线y＝ax2＋bx－3(a≠0)与x轴交于A，B两点，与y轴交于点C，且BO＝OC＝3AO，连接BC.

(1)求抛物线的表达式；

(2)在抛物线的对称轴上是否存在点P，使△PBC是等腰三角形？若存在，试求出符合条件的P点坐标；若不存在，请说明理由．

如图，已知抛物线y=﹣x2+bx+c与x轴交于点A（﹣1，0）和点B（3，0），与y轴交于点C，连接BC交抛物线的对称轴于点E，D是抛物线的顶点．

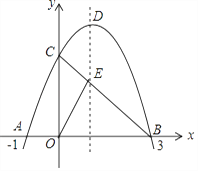
（1）求此抛物线的解析式；

（2）直接写出点C和点D的坐标；

（3）若点P在第一象限内的抛物线上，且S△ABP=4S△COE ， 求P点坐标．

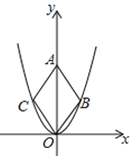
二次函数y=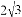x2的图象如图，点O为坐标原点，点A在y轴的正半轴上，点B、C在二次函数y=x2的图象上，四边形OBAC为菱形，且∠OBA=120°，则菱形OBAC的面积是______．

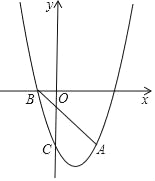
如图，抛物线y=ax2+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y轴交于点C，且OC=3OB．

（1）求抛物线的解析式；

（2）点D在y轴上，且∠BDO=∠BAC，求点D的坐标；

（3）点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．

如图，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则凸轮的周长等于　 　．

（2016·湘潭中考）已知以点C（a，b）为圆心，半径为r的圆的标准方程为（x－a）2＋（y－b）2＝r2.例如：以A（2，3）为圆心，半径为2的圆的标准方程为（x－2）2＋（y－3）2＝4，则以原点为圆心，过点P（1，0）的圆的标准方程为____.

在?ABCD中，AD=8，AE平分∠BAD交BC于点E，DF平分∠ADC交BC于点F，且EF=2，则AB的长为（　　）

A. 3 B. 5 C. 2或3 D. 3或5

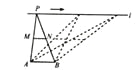
如图，点A，B为定点，定直线l//AB，P是l上一动点．点M，N分别为PA，PB的中点，对于下列各值：

①线段MN的长；

②△PAB的周长；

③△PMN的面积；

④直线MN，AB之间的距离；

⑤∠APB的大小．

其中会随点P的移动而变化的是（ ）

A. ②③ B. ②⑤ C. ①③④ D. ④⑤

如图，在△ABC中，∠ABC=90°，AB=8，BC=6．若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（　 　）

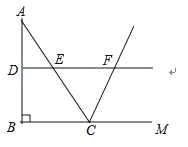
A. 7 B. 8 C. 9 D. 10

如图，在矩形ABCD中（AD＞AB），点E是BC上一点，且DE=DA，AF⊥DE，垂足为点F，在下列结论中，不一定正确的是（ ）

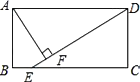
A. △AFD≌△DCE B. AF=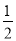AD C. AB=AF D. BE=AD﹣DF