
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:填空题
对于函数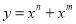 ,我们定义
,我们定义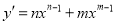 (
(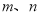 为常数).
为常数).
例如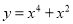 ,则
,则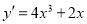 .
.
已知: 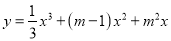 .
.
(1)若方程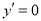 有两个相等实数根,则
有两个相等实数根,则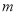 的值为___________;
的值为___________;
(2)若方程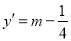 有两个正数根,则
有两个正数根,则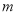 的取值范围为__________.
的取值范围为__________.
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:填空题
阅读理【解析】
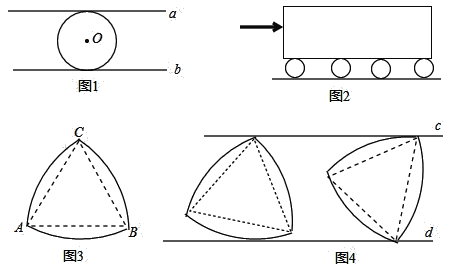
如图1,⊙O与直线a、b都相切,不论⊙O如何转动,直线a、b之间的距离始终保持不变(等于⊙O的直径),我们把具有这一特性的图形成为“等宽曲线”,图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力既可以推动物体前进,据说,古埃及人就是利用这样的方法将巨石推到金字塔顶的.
拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”,如图4,夹在平行线c,d之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变,若直线c,d之间的距离等于2cm,则莱洛三角形的周长为________cm.
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:填空题
高斯函数[x],也称为取整函数,即[x]表示不超过x的最大整数.
例如:[2.3]=2,[﹣1.5]=﹣2.
则下列结论:
①[﹣2.1]+[1]=﹣2;
②[x]+[﹣x]=0;
③若[x+1]=3,则x的取值范围是2≤x<3;
④当﹣1≤x<1时,[x+1]+[﹣x+1]的值为0、1、2.
其中正确的结论有________(写出所有正确结论的序号).
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:填空题
已知点P是△ABC内一点,且它到三角形的三个顶点距离之和最小,则P点叫△ABC的费马点(Fermat point),已经证明:在三个内角均小于120°的△ABC中,当∠APB=∠APC=∠BPC=120°时,P就是△ABC的费马点,若P就是△ABC的费马点,若点P是腰长为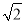 的等腰直角三角形DEF的费马点,则PD+PE+PF= .
的等腰直角三角形DEF的费马点,则PD+PE+PF= .
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:填空题
平面直角坐标系中有两点M(a,b),N(c,d),规定(a,b)⊕(c,d)=(a+c,b+d),则称点Q(a+c,b+d)为M,N的“和点”.若以坐标原点O与任意两点及它们的“和点”为顶点能构成四边形,则称这个四边形为“和点四边形”,现有点A(2,5),B(﹣1,3),若以O,A,B,C四点为顶点的四边形是“和点四边形”,则点C的坐标是___________。
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:填空题
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A,B,C,D分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x2-2x-3,AB为半圆的直径,则这个“果圆”被y轴截得的弦CD的长为____.
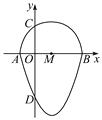
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:填空题
(2015湖州)如图,已知抛物线C1: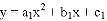 和C2:
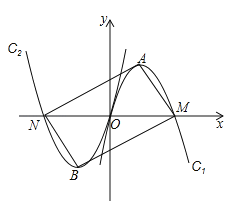
和C2: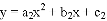 都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是____________________和__________________.
都经过原点,顶点分别为A,B,与x轴的另一交点分别为M,N,如果点A与点B,点M与点N都关于原点O成中心对称,则称抛物线C1和C2为姐妹抛物线,请你写出一对姐妹抛物线C1和C2,使四边形ANBM恰好是矩形,你所写的一对抛物线解析式是____________________和__________________.
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:解答题
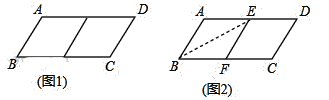
邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,?ABCD中,若AB=1,BC=2,则?ABCD为1阶准菱形.
(1)猜想与计算:
邻边长分别为3和5的平行四边形是_______阶准菱形;已知?ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出?ABCD___________阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把?ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
科目: 来源:2017-2018学年中考数学经典题型训练卷:新定义阅读问题 题型:解答题
我们知道,任意一个正整数n都可以进行这样的分【解析】
n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解.并规定:F(n)= .
.
例如12可以分解成1×12,2×6或3×4,因为12﹣1>6﹣2>4﹣3,所以3×4是12的最佳分解,所以F(12)= .
.
(1)如果一个正整数m是另外一个正整数n的平方,我们称正整数m是完全平方数.
求证:对任意一个完全平方数m,总有F(m)=1;
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36,那么我们称这个数t为“吉祥数”,求所有“吉祥数”;
(3)在(2)所得“吉祥数”中,求F(t)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com