
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:解答题
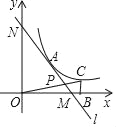
如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,4),点A为MN的中点,反比例函数y=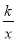 (x>0)的图象过点A.
(x>0)的图象过点A.
(1)求直线l和反比例函数的解析式;
(2)在函数y=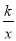 (k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
(k>0)的图象上取异于点A的一点C,作CB⊥x轴于点B,连接OC交直线l于点P,若△ONP的面积是△OBC面积的3倍,求点P的坐标.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:解答题
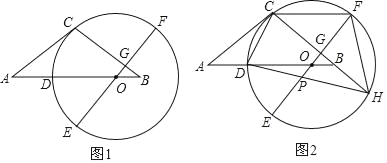
如图1,等腰△ABC中,AC=BC,点O在AB边上,以O为圆心的圆经过点C,交AB边于点D,EF为⊙O的直径,EF⊥BC于点G,且D是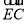 的中点.
的中点.
(1)求证:AC是⊙O的切线;
(2)如图2,延长CB交⊙O于点H,连接HD交OE于点P,连接CF,求证:CF=DO+OP;
(3)在(2)的条件下,连接CD,若tan∠HDC=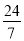 ,CG=4,求OP的长.
,CG=4,求OP的长.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:填空题
已知关于x的一元二次方程x2﹣mx+2m﹣1=0的两根x1、x2满足x12+x22=14,则m=_____
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:填空题
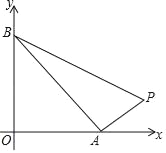
如图,由点P(14,1),A(a,0),B(0,a)(0<a<14)确定的△PAB的面积为18,则a的值为_____.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:填空题
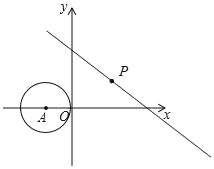
如图,在直角坐标系中,⊙A的圆心的坐标为(﹣2,0),半径为2,点P为直线y=﹣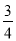 x+6上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是_____.
x+6上的动点,过点P作⊙A的切线,切点为Q,则切线长PQ的最小值是_____.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:填空题
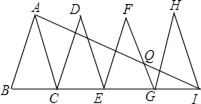
如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI=_____.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:填空题
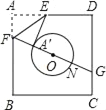
如图,已知正方形ABCD的边长是⊙O半径的4倍,圆心O是正方形ABCD的中心,将纸片按图示方式折叠,使EA'恰好与⊙O相切于点A',则tan∠A'FE的值为_____.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:解答题
某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:解答题
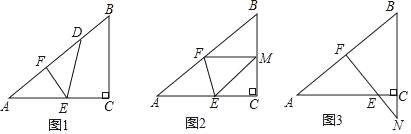
如图,已知一个三角形纸片ACB,其中∠ACB=90°,AC=8,BC=6,E、F分别是AC、AB边上的点,连接EF.(1)如图1,若将纸片ACB的一角沿EF折叠,折叠后点A落在AB边上的点D处,且使S四边形ECBF=4S△EDF,求ED的长;
(2)如图2,若将纸片ACB的一角沿EF折叠,折叠后点A落在BC边上的点M处,且使MF∥CA.
①试判断四边形AEMF的形状,并证明你的结论;
②求EF的长;
(3)如图3,若FE的延长线与BC的延长线交于点N,CN=2,CE=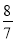 ,求
,求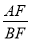 的值.
的值.
查看答案和解析>>
科目: 来源:四川省成都市青羊区2017-2018学年中考一诊数学试卷 题型:解答题
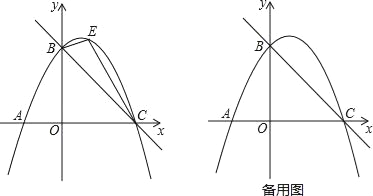
如图,直线y=﹣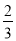 x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+
x+4与x轴交于点C,与y轴交于点B,抛物线y=ax2+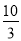 x+c经过B、C两点.
x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标;
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com