
科目: 来源:浙江省湖州市2018届九年级中考数学模拟试卷 题型:填空题
已知一组数据a1,a2,a3,a4的平均数是2017,则另一组数据a1+3,a2﹣2,a3﹣2,a4+5的平均数是_____.
查看答案和解析>>
科目: 来源:浙江省湖州市2018届九年级中考数学模拟试卷 题型:填空题
(2017浙江省湖州市)如图,已知∠AOB=30°,在射线OA上取点O1,以O1为圆心的圆与OB相切;在射线O1A上取点O2,以O2为圆心,O2O1为半径的圆与OB相切;在射线O2A上取点O3,以O3为圆心,O3O2为半径的圆与OB相切;…;在射线O9A上取点O10,以O10为圆心,O10O9为半径的圆与OB相切.若⊙O1的半径为1,则⊙O10的半径长是______.
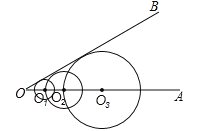
查看答案和解析>>
科目: 来源:浙江省湖州市2018届九年级中考数学模拟试卷 题型:解答题
对于任意实数a,b,定义关于“?”的一种运算如下:a?b=2a﹣b.例如:5?2=2×5﹣2=8,(﹣3)?4=2×(﹣3)﹣4=﹣10.
(1)若3?x=﹣2011,求x的值;
(2)若x?3<5,求x的取值范围.
查看答案和解析>>
科目: 来源:浙江省湖州市2018届九年级中考数学模拟试卷 题型:填空题
为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
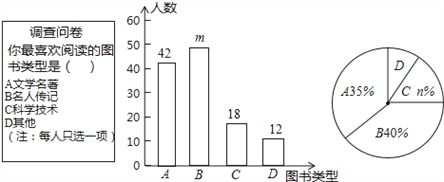
(1)本次调查共抽查了 名学生;
(2)两幅统计图中的m= ,n= .
(3)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
查看答案和解析>>
科目: 来源:浙江省湖州市2018届九年级中考数学模拟试卷 题型:解答题
一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果,并求出点P(x,y)落在第三象限的概率.
查看答案和解析>>
科目: 来源:浙江省湖州市2018届九年级中考数学模拟试卷 题型:解答题
定义:如图1,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点,点P在该抛物线上(点P与A、B两点不重合),如果△ABP的三边满足AP2+BP2=AB2,则称点P为抛物线y=ax2+bx+c(a≠0)的勾股点.
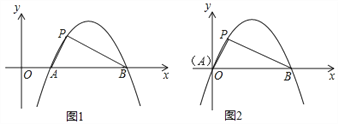
(1)直接写出抛物线y=–x2+1的勾股点的坐标;
(2)如图2,已知抛物线C:y=ax2+bx(a≠0)与x轴交于A,B两点,点P(1,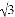 )是抛物线C的勾股点,求抛物线C的函数表达式;
)是抛物线C的勾股点,求抛物线C的函数表达式;
(3)在(2)的条件下,点Q在抛物线C上,求满足条件S△ABQ=S△ABP的Q点(异于点P)的坐标.
查看答案和解析>>
科目: 来源:浙江省湖州市2018届九年级中考数学模拟试卷 题型:解答题
问题背景
如图1,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
类比探究
如图2,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合)
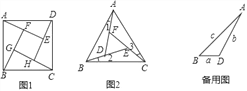
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明.
(2)△DEF是否为正三角形?请说明理由.
(3)进一步探究发现,△ABD的三边存在一定的等量关系,设BD=a,AD=b,AB=c,请探索a,b,c满足的等量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com