
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:填空题
平面直角坐标系中,点A、B的坐标分别为(4,0)、(0,4),点D为OB上任意一点,连接AD,以OD为直径的圆交AD于点E,则当线段BE的长最短时E的坐标为________.
查看答案和解析>>
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:解答题
某校为迎接体育中考,了解学生的体育情况,学校随机调查了本校九年级50名学生“30秒跳绳”的次数,并将调查所得的数据整理如下:

成绩段 | 频数 | 频率 |
0≤x<20 | 5 | 0.1 |
20≤x<40 | 10 | a |
40≤x<60 | b | 0.14 |
60≤x<80 | m | c |
80≤x<100 | 12 | n |


根据以上图表信息,解答下列问题:
(1)表中的a= ,m= ;
(2)请把频数分布直方图补充完整;(画图后请标注相应的数据)
(3)若该校九年级共有600名学生,请你估计“30秒跳绳”的次数60次以上(含60次)的学生有多人?
查看答案和解析>>
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:解答题
在某小学“演讲大赛”选拔赛初赛中,甲、乙、丙三位评委对小选手的综合表现,分别给出“待定”(用字母W表示)或“通过”(用字母P表示)的结论.
⑴请用树状图表示出三位评委给小选手琪琪的所有可能的结论;
⑵对于小选手琪琪,只有甲、乙两位评委给出相同结论的概率是多少?
⑶比赛规定,三位评委中至少有两位给出“通过”的结论,则小选手可入围进入复赛,问琪琪进入复赛的概率是______________.
查看答案和解析>>
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:解答题
已知,如图,线段AB,利用无刻度的直尺和圆规,作一个满足条件的△ABC:
① ∠ACB为直角 ②sin∠A= . (注:不要求写作法,但保留作图痕迹)
. (注:不要求写作法,但保留作图痕迹)

查看答案和解析>>
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:解答题
今年我市某公司分两次采购了一批大蒜,第一次花费40万元,第二次花费60万元.已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元,第二次采购时每吨大蒜的价格比去年的平均价格下降了500元,第二次的采购数量是第一次采购数量的两倍.
(1)试问去年每吨大蒜的平均价格是多少元?
(2)该公司可将大蒜加工成蒜粉或蒜片,若单独加工成蒜粉,每天可加工8吨大蒜,每吨大蒜获利1000元;若单独加工成蒜片,每天可加工12吨大蒜,每吨大蒜获利600元.由于出口需要,所有采购的大蒜必需在30天内加工完毕,且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半,为获得最大利润,应将多少吨大蒜加工成蒜粉?最大利润为多少?
查看答案和解析>>
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:解答题
已知二次函数y=a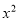 -8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
-8ax(a<0)的图像与x轴的正半轴交于点A,它的顶点为P.点C为y轴正半轴上一点,直线AC与该图像的另一交点为B,与过点P且垂直于x轴的直线交于点D,且CB:AB=1:7.
(1)求点A的坐标及点C的坐标(用含a的代数式表示);
(2)连接BP,若△BDP与△AOC相似(点O为原点),求此二次函数的关系式.
查看答案和解析>>
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:解答题
如图,在△ABC中,已知AB=AC=10cm,BC=16cm,AD⊥BC于D,点E、F分别从B、C两点同时出发,其中点E沿BC向终点C运动,速度为4cm/s;点F沿CA、AB向终点B运动,速度为5cm/s,设它们运动的时间为x(s).

(1)求x为何值时,△EFC和△ACD相似;
(2)是否存在某一时刻,使得△EFD被 AD分得的两部分面积之比为3:5,若存在,求出x的值,若不存在,请说明理由;
(3)若以EF为直径的圆与线段AC只有一个公共点,求出相应x的取值范围.
查看答案和解析>>
科目: 来源:江阴市2017-2018学年第二学期5月初三数学模拟试卷 题型:解答题
阅读理【解析】
小明热爱数学,在课外书上看到了一个有趣的定理——“中线长定理”:三角形两边的平方和等于第三边的一半与第三边上的中线的平方和的两倍.如图1,在△ABC中,点D为BC的中点,根据“中线长定理”,可得:
AB2+AC2=2AD2+2BD2.
小明尝试对它进行证明,部分过程如下:
【解析】
过点A作AE⊥BC于点E,如图2,在Rt△ABE中,AB2=AE2+BE2,
同理可得:AC2=AE2+CE2,AD2=AE2+DE2,
为证明的方便,不妨设BD=CD=x,DE=y,
∴AB2+AC2=AE2+BE2+AE2+CE2=……
(1)请你完成小明剩余的证明过程;

理解运用:
(2) ① 在△ABC中,点D为BC的中点,AB=6,AC=4,BC=8,则AD=_______;
② 如图3,⊙O的半径为6,点A在圆内,且OA=2 ,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
,点B和点C在⊙O上,且∠BAC=90°,点E、F分别为AO、BC的中点,则EF的长为________;
拓展延伸:
(3)小明解决上述问题后,联想到《能力训练》上的题目:如图4,已知⊙O的半径为5 ,以A(?3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.
,以A(?3,4)为直角顶点的△ABC的另两个顶点B,C都在⊙O上,D为BC的中点,求AD长的最大值.请你利用上面的方法和结论,求出AD长的最大值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com