⑴ 阅读理解

问题1：已知a、b、c、d为正数，，ac=bd，试说明a=d，b=c.

我们通过构造几何模型解决代数问题. 注意到条件，如果把a、b、c、d分别看作为两个直角三角形的直角边，那么可构造图1所示的几何模型.

∵ac=bd,

∴AB·CD=BC·AD

∴

请你按照以上思路继续完成说明.

⑵ 深入探究

问题2：若a＞0，b＞0，试比较和的大小.

为此我们构造图2所示的几何模型，其中AB为直径, O为圆心，点C在半圆上，CD⊥AB 于D，AD＝a，BD＝b.

请你利用图2所示的几何模型解决提出的问题2．

⑶ 拓展运用

对于函数y=x+，求当x＞0时，求y的取值范围．

如图，在边长为2的正方形ABCD中，点P是边AD上的动点（点P不与点A、点D重合），点Q是边CD上一点，连接PB、PQ，且∠PBC＝∠BPQ．

⑴ 若tan∠PBC=4，求AP的长；

⑵ 是否存在点P，使得点Q恰好是边CD的中点？若存在，求出AP的长；若不存在，请说明理由．⑶ 连接BQ，在△PBQ中是否存在度数不变的角？若存在，指出这个角，并求出它的度数；若不存在，请说明理由．

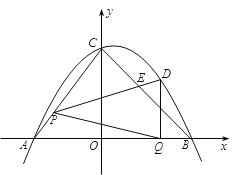
如图，在平面直角坐标系中，已知A（－3，0），B（4，0），C（0，4）. 二次函数的图像经过A、B、C三点．点P沿AC由点A处向点C运动，同时，点Q沿BO由点B处向点O运动，运动速度均为每秒1个单位长度.当一个点停止运动时，另一个点也随之停止运动．连接PQ，过点Q作QD⊥x轴，与二次函数的图像交于点D，连接PD，PD与BC交于点E． 设点P的运动时间为t秒（t＞0）.

⑴ 求二次函数的表达式； 

⑵ 在点P、Q运动的过程中，当∠PQA＋∠PDQ＝90°时，求t的值； 

⑶ 连接PB、BD、CD，试探究在点P，Q运动的过程中，是否存在某一时刻，使得四边形PBDC是平行四边形？若存在，请求出此时t的值与点E的坐标；若不存在，请说明理由.

对于抛物线y＝－x2＋2x＋3，有下列四个结论：①它的对称轴为x＝1；

②它的顶点坐标为(1，4)；

③它与y轴的交点坐标为(0，3)，与x轴的交点坐标为(－1，0)和(3，0)；

④当x＞0时，y随x的增大而减小．

其中正确的个数为(　　)

A. 1 B. 2 C. 3 D. 4

小张同学说出了二次函数的两个条件：

(1)当x＜1时，y随x的增大而增大；

(2)函数图象经过点(－2，4)．

则符合条件的二次函数表达式可以是(　 　)

A. y＝－(x－1)2－5 B. y＝2(x－1)2－14

C. y＝－(x＋1)2＋5 D. y＝－(x－2)2＋20

求下列函数的图象的对称轴、顶点坐标及与x轴的交点坐标．

(1)y＝4x2＋24x＋35；

(2)y＝－3x2＋6x＋2；

(3)y＝x2－x＋3；

(4)y＝2x2＋12x＋18.

将抛物线y＝－2x2＋1向右平移1个单位长度，再向上平移1个单位长度所得的抛物线解析式为(　　)

A. y＝－2(x＋1)2 B. y＝－2(x＋1)2＋2

C. y＝－2(x－1)2＋2 D. y＝－2(x－1)2＋1

将抛物线y＝2x2＋4x－5的图象向左平移2个单位，再向上平移1个单位，所得抛物线表达式是(　 　)

A. y＝2(x＋1)2－7 B. y＝2(x＋1)2－6

C. y＝2(x＋3)2－6 D. y＝2(x－1)2－6

若二次函数y＝x2－2x＋m的图象与x轴有两个交点，则m的取值范围是_______．

已知二次函数y＝x2－2x＋m(m为常数)的图象与x轴的一个交点为(－1，0)，则关于x的一元二次方程x2－2x＋m＝0的两个实数根是(　　)

A. x1＝1，x2＝2 B. x1＝1，x2＝3

C. x1＝－1，x2＝2 D. x1＝－1，x2＝3