
科目: 来源:北京市朝阳区2017-2018学年七年级第二学期期末考试数学试卷 题型:解答题
如图,在□ABCD中,∠ABC,∠BCD的平分线分别交AD于点E,F,BE,CF相交于点G.
(1)求证:BE⊥CF;
(2)若AB=a,CF=b,写出求BE的长的思路.

查看答案和解析>>
科目: 来源:北京市朝阳区2017-2018学年七年级第二学期期末考试数学试卷 题型:解答题
甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90

(1)请根据乙校的数据补全条形统计图;
(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,
请为他们各写出一条可以使用的理由;
甲校: .乙校: .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
查看答案和解析>>
科目: 来源:北京市朝阳区2017-2018学年七年级第二学期期末考试数学试卷 题型:解答题
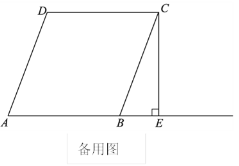
如图,在菱形ABCD中,CE⊥AB交AB延长线于点E,点F为点B关于CE的对称点,连接CF,分别延长DC,CF至点G,H,使FH=CG,连接AG,DH交于点P.
(1)依题意补全图1;
(2)猜想AG和DH的数量关系并证明;
(3)若∠DAB=70°,是否存在点G,使得△ADP为等边三角形?若存在,求出CG的长;若不存在,说明理由.

查看答案和解析>>
科目: 来源:北京市朝阳区2017-2018学年七年级第二学期期末考试数学试卷 题型:解答题
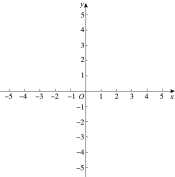
在平面直角坐标系xOy中,对于与坐标轴不平行的直线l和点P,给出如下定义:过点P作x轴,y轴的垂线,分别交直线l于点M,N,若PM+PN≤4,则称P为直线l的近距点,特别地,直线上l所有的点都是直线l的近距点.已知点A(-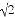 ,0),B(0,2),C(-2,2).
,0),B(0,2),C(-2,2).
(1)当直线l的表达式为y=x时,
①在点A,B,C中,直线l的近距点是 ;
②若以OA为边的矩形OAEF上所有的点都是直线l的近距点,求点E的纵坐标n的取值范围;
(2)当直线l的表达式为y=kx时,若点C是直线l的近距点,直接写出k的取值范围.
查看答案和解析>>
科目: 来源:北师大版九年级数学上册第二章 一元二次方程 练习题 题型:单选题
下列方程中,没有实数根的是( )
A. x2﹣2x=0 B. x2﹣2x﹣1=0 C. x2﹣2x+1 =0 D. x2﹣2x+2=0
查看答案和解析>>
科目: 来源:北师大版九年级数学上册第二章 一元二次方程 练习题 题型:单选题
一元二次方程x2-8x=48可表示成(x-a)2=48+b的形式,其中a,b为整数,求a+b之值为何( )
A. 20 B. 12 C. -12 D. -20
查看答案和解析>>
科目: 来源:北师大版九年级数学上册第二章 一元二次方程 练习题 题型:单选题
已知关于x的方程x2+x﹣a=0的一个根为2,则另一个根是( )
A. ﹣3 B. ﹣2 C. 3 D. 6
查看答案和解析>>
科目: 来源:北师大版九年级数学上册第二章 一元二次方程 练习题 题型:单选题
“一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,在论坛召开之际,福田欧辉陆续向缅甸仰光公交公司交付1000台清洁能源公交车,以2017客车海外出口第一大单的成绩,创下了客车行业出口之最,同时,这也是在国家“一带一路”战略下,福田欧辉代表“中国制造”走出去的成果.预计到2019年,福田公司将向海外出口清洁能源公交车达到3000台.设平均每年的出口增长率为x,可列方程为( )
A. 1000(1+x%)2=3000 B. 1000(1﹣x%)2=3000 C. 1000(1+x)2=3000 D. 1000(1﹣x)2=3000
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com