
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
我们给出如下定义:如图①,平面内两条直线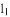 、
、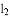 相交于点O,对于平面内的任意一点M,若p、q分别是点M到直线
相交于点O,对于平面内的任意一点M,若p、q分别是点M到直线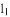 和
和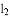 的距离(P≥0,q≥0
的距离(P≥0,q≥0
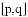 是点M的距离坐标。
是点M的距离坐标。
根据上述定义,请解答下列问题:
如图②,平面直角坐标系xoy内,直线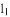 的关系式为
的关系式为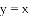
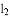 的关系式为
的关系式为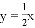 ,M是平面直角坐标系内的点。
,M是平面直角坐标系内的点。
(1)若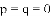
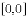 时,点M的坐标;
时,点M的坐标;
(2)若
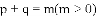
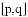 时,点M的坐标;
时,点M的坐标;
(3)若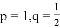 ,则坐标平面内距离坐标为
,则坐标平面内距离坐标为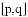 时,点M可以有几个位置?并用三角尺在图③画出符合条件的点M(简要说明画法)。
时,点M可以有几个位置?并用三角尺在图③画出符合条件的点M(简要说明画法)。
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
我市某镇组织20辆汽车装运完A、B、C三种脐橙共100吨到外地销售.按计划,20辆汽车都要装运,每辆汽车只能装运同一种脐橙,且必须装满.根据下表提供的信息,解答以下问题:

(1)设装运A种脐橙的车辆数为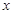 ,装运B种脐橙的车辆数为
,装运B种脐橙的车辆数为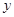 ,求
,求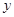 与
与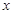 之间的函数关系式;
之间的函数关系式;
(2)如果装运每种脐橙的车辆数都不少于4辆,那么车辆的安排方案有几种?并写出每种安排方案;
(3)若要使此次销售获利最大,应采用哪种安排方案?并求出最大利润的值.
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
如图①,在矩形ABCD中,AB=10 cm,BC=8 cm.点P从点A出发,沿A→B→C→D的路线运动,到点D停止;点Q从点D出发,沿D→C→B→A的路线运动,到点A停止.若点P、点Q同时出发,点P的速度为每秒1 cm,点Q的速度为每秒2 cm,a秒时,点P、点Q同时改变速度,点P的速度变为每秒b cm,点Q的速度变为每秒d cm.图②是点P出发x秒后△APD的面积S1(cm2)与时间x(秒)的函数关系图象;图③是点Q出发x秒后△AQD的面积S2(cm2)与时间x(秒)的函数关系图象.
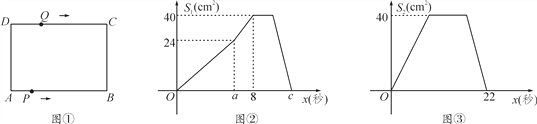
(1)参照图②,求a、 b及图②中c的值;
(2)求d的值;
(3)设点P离开点A的路程为y1(cm),点Q到点A还需要走的路程为y2(cm),请分别写出改变速度后,y1、y2与出发后的运动时间x(秒)的函数关系式,并求出点P、点Q相遇时x的值;
(4)当点Q出发__ __秒时,点Q的运动路程为25 cm.
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
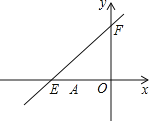
如图,直线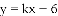
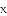
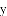
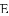
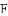
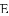
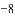
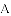
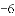
(1)求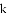
(2)若点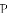
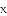
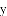
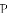
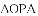
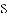
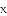
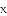
(3)探究:当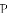
 ,并说明理由.
,并说明理由.
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
甲骑自行车、乙骑摩托车沿相同路线由A地到B地,行驶过程中路程与时间的函数关系的图象如图. 根据图象解决下列问题:
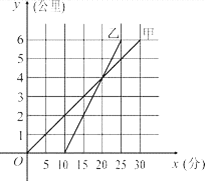
(1) 谁先出发?先出发多少时间?谁先到达终点?先到多少时间?
(2) 分别求出甲、乙两人的行驶速度;
(3) 在什么时间段内,两人均行驶在途中(不包括起点和终点)?在这一时间段内,请你根据下列情形,分别列出关于行驶时间x的方程或不等式(不化简,也不求解):① 甲在乙的前面;② 甲与乙相遇;③ 甲在乙后面.
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
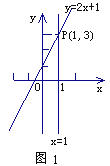
阅读,我们知道,在数轴上,x=1表示一个点,而在平面坐标系中,x=1表示一条直线;我们还知道,以二元一次方程2x-y+1=0的所有解为坐标的点组成的图形,就是一次函数y=2x+1的图象,它也是一条直线,如图1,可以得出,直线x=1与直线y=2x+1的交点P的坐标(1,3)就是方程组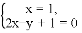 的解,所以这个方程组的解为
的解,所以这个方程组的解为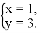
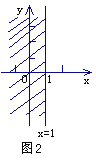
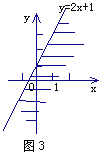
在直角坐标系中,x≤1表示一个平面区域,即直线x=1以及它的左侧的部分,如图2;y≤2x+1,也表示一个平面区域,即直线y=2x+1以及它下方的部分,如图3.
回答下列问题:
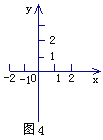
(1)在直角坐标系(如图4)中,用作图的方法求方程组 的解;
的解;
(2)用阴影表示 所围成的区域.
所围成的区域.
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
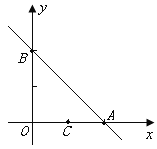
如图,已知直线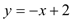 与
与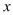 轴、
轴、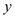 轴交点分别为
轴交点分别为 、
、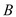 ,另一直线
,另一直线
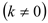 经过
经过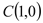 ,且把
,且把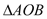 分成两部分.
分成两部分.
(1)若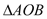 被分成的两部分面积相等,求
被分成的两部分面积相等,求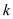 和
和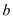 的值.
的值.
(2)若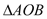 被分成的两部分面积之比为
被分成的两部分面积之比为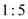 ,求
,求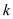 和
和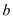 的值.
的值.
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
在某地,人们发现某种蟋蟀1min,所叫次数x与当地温度T之间的关系或为T=ax+b,下面是蟋蟀所叫次数与温度变化情况对照表:
蟋蟀叫的次数(x) | … | 84 | 98 | 119 | … |
温度(℃)T | … | 15 | 17 | 20 | … |
①根据表中的数据确定a、b的值.
②如果蟋蟀1min叫63次,那么该地当时的温度约为多少摄氏度?
查看答案和解析>>
科目: 来源:人教版八年级下册 第十九章《一次函数综合应用》提高检测试卷 题型:解答题
某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门.乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元.
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量x的取值范围.
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com