
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:填空题
如图所示,E,D是AB,AC上的两点,BD,CE交于点O,且AB=AC,使△ACE≌△ABD,你补充的条件是________
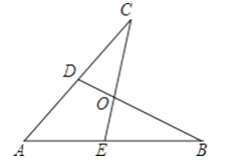
查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:填空题
如图,有一个直角△ABC,∠C=90°,AC=6,BC=3,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,问:当AP=________时,才能使以点P、A、Q为顶点的三角形与△ABC全等.
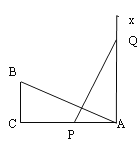
查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
已知:如图点A、B、C、D在一条直线上,EA∥FB,EC∥FD,AB=CD,求证:EA=FB.

查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
在图示的方格纸中,(1)画出△ABC关于MN对称的图形△A1B1C1;
(2)说明△A2B2C2是由△A1B1C1经过怎样的平移得到的?
(3)在直线MN上找一点P,使得PB+PA最短.(不必说明理由).
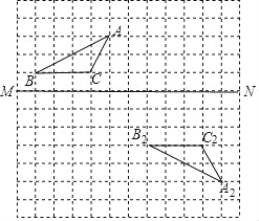
查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
如图,已知:在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD.图中的CE、BD有怎样的大小和位置关系?试证明你的结论.
查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
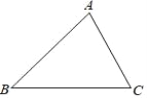
某国际帆船中心外形形状是一个三角形,要在它的内部修建一处公共服务设施(用点P表示),使它到三条路AB、BC、AC的距离相等.
(1)在图中确定公共服务设施P的位置.(不写作法,保留作图痕迹)
(2)若∠BAC=78°,试求∠BPC的度数.
查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
如图,△ABC中,AD平分∠BAC,DG⊥BC且平分BC,DE⊥AB于E,DF⊥AC于F.
(1)求证:BE=CF;
(2)如果AB=8,AC=6,求AE、BE的长.

查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
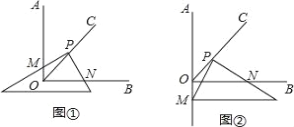
已知∠AOB=90°,OC是∠AOB的平分线,按以下要求解答问题.
(1)将三角板的直角顶点P在射线OC上移动,两直角边分别与OA,OB交于M,N,如图①,求证:PM=PN;
(2)将三角板的直角顶点P在射线OC上移动,一条直角边与OB交于N,另一条直角边与射线OA的反向延长线交于点M,并猜想此时①中的结论PM=PN是否成立,并说明理由 .
查看答案和解析>>
科目: 来源:江苏省东台市第五联盟2018-2019学年八年级上学期第一次月考数学试卷 题型:解答题
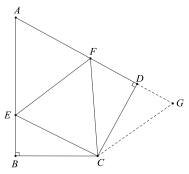
(题文)(问题引领)
问题1:在四边形ABCD中,CB=CD,∠B=∠ADC=90°,∠BCD=120°.E,F分别是AB,AD上的点.且∠ECF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结CG,先证明
△CBE≌△CDG,再证明△CEF≌△CGF.他得出的正确结论是________________.
(探究思考)
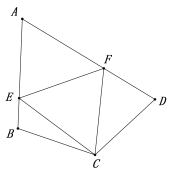
问题2:若将问题1的条件改为:四边形ABCD中,CB=CD,∠ABC+∠ADC=180°,
∠ECF=  ∠BCD, 问题1的结论是否仍然成立?请说明理由.
∠BCD, 问题1的结论是否仍然成立?请说明理由.
(拓展延伸)
问题3:在问题2的条件下,若点E在AB的延长线上,点F在DA的延长线上,则问题2的结论是否仍然成立?若不成立,猜测此时线段BE、DF、EF之间存在什么样的等量关系?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com