
 已知第20天时,该商品的单价为27元,40天时,该商品的单价为32元.
已知第20天时,该商品的单价为27元,40天时,该商品的单价为32元. .求这种商品在这100天内哪一天的销售额y最高?最高为多少(精确到1元)?
.求这种商品在这100天内哪一天的销售额y最高?最高为多少(精确到1元)? ,
,

 .
. 


 是减函数,∴
是减函数,∴


科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 109 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
|
| 1 |
| 3 |
| 112 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
经市场调查,某商品在近100天内其销售量和价格均是时间t的函数,且销售量近似地满足关系:g(t)=-![]() t+
t+![]() (t∈N*,0<t≤100).在前40天内价格为f(t)=
(t∈N*,0<t≤100).在前40天内价格为f(t)=![]() t+22(t∈N*,0<t≤40);在后60天内价格为f(t)=
t+22(t∈N*,0<t≤40);在后60天内价格为f(t)=
- ![]() t+52(t∈N*,40<t≤100).求这种商品的日销售额的最大值(精确到1).
t+52(t∈N*,40<t≤100).求这种商品的日销售额的最大值(精确到1).
查看答案和解析>>
科目:高中数学 来源: 题型:
某商品在近100天内,商品的单价f(t)(元)与时间t(天)的函数关系式如下:
f(t)=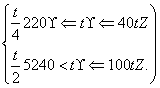
销售量g(t)与时间t(天)的函数关系式是
g(t)=-![]() +
+![]() (0≤t≤100,t∈Z).
(0≤t≤100,t∈Z).
求这种商品在这100天内哪一天的销售额最高?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com