定义在(－1，1)上的函数f(x)，(i)对任意x，(－1，1)都有：；(ii)当(－1，0)时，f(x)＞0，回答下列问题．

(1)判断f(x)在(－1，1)上的奇偶性，并说明理由．

(2)判断函数f(x)在(0，1)上的单调性，并说明理由．

(3)(理)若，试求的值．

某森林出现火灾，火势正以每分钟100 m²的速度顺风蔓延，消防站接到警报立即派消防队员前去，在火灾发生后五分钟到达救火现场，已知消防队员在现场平均每人每分钟灭火50 m²，所消耗的灭火材料、劳务津贴等费用为每人每分钟125元，另附加每次救火所耗损的车辆、器械和装备等费用平均每人100元，而烧毁一平方米森林损失费为60元．问应该派多少消防队员前去救火，才能使总损失最少？

如图，在正三棱柱ABC－A₁B₁C₁中，M，N分别为A₁B₁，BC之中点．

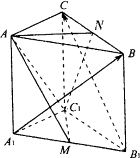
(1)试求，使．

(2)在(1)条件下，求二面角N－AC₁－M的大小．

已知数列{a_n}的前n项和为S_n，且满足条件：4S_n＝＋4n－1，n∈N*．

(1)证明：(a_n－2)²－＝0(n≥2)；

(2)满足条件的数列不惟一，试至少求出数列{a_n}的的3个不同的通项公式．

已知，函数．

(Ⅰ)如果函数是偶函数，求f(x)的极大值和极小值；

(Ⅱ)如果函数f(x)是(－∞，＋∞)上的单调函数，求a的取值范围．

已知数列{a_n}是等比数列，a₄＝e，如果a₂，a₇是关于x的方程：ex²＋kx＋1＝0，两个实根，(e是自然对数的底数)

(1)求{a_n}的通项公式；

(2)设：b_n＝lna_n，S_n是数列{b_n}的前n项的和，当：S_n＝n时，求n的值；

(3)对于(2)中的{b_n}，设：cn＝b_nb_n+1b_n+2，而T_n是数列{c_n}的前n项和，求T_n的最大值，及相应的n的值．

如图，已知直线l与抛物线x²＝4y相切于点P(2，1)，且与x轴交于点A，O为坐标原点，定点B的坐标为(2，0)．

(1)若动点M满足，求点M的轨迹C；

(2)若过点B的直线(斜率不等于零)与(I)中的轨迹C交于不同的两点E、F(E在B、F之间)，试求△OBE与△OBF面积之比的取值范围．

已知数列{a_n}的前n项和S_n满足：(a为常数，且a≠0，a≠1)．

(1)求{a_n}的通项公式；

(2)设，若数列{b_n}为等比数列，求a的值；

(3)在满足条件(Ⅱ)的情形下，设，数列{c_n}的前n项和为T_n．求证：．

如图所示，四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，PD＝AB＝2，E，F，G分别为PC、PD、BC的中点．

(1)求证：PA⊥EF；

(2)求二面角D－FG－E的余弦值．

已知点A，B的坐标分别是(0，－1)，(0，1)，直线AM，BM相交于点M，且它们的斜率之积为．

(1)求点M轨迹C的方程；

(2)若过点D(2，0)的直线l与(1)中的轨迹C交于不同的两点E、F(E在D、F之间)，试求△ODE与△ODF面积之比的取值范围(O为坐标原点)．