某汽车驾驶学校在学员结业前，对学员的驾驶技术进行4次考核，规定：按顺序考核，一旦考核合格就不必参加以后的考核，否则还需参加下次考核．若学员小李独立参加每次考核合格的概率依次组成一个公差为的等差数列，他参加第一次考核合格的概率不超过，且他直到参加第二次考核才合格的概率为．

求小李第一次参加考核就合格的概率p₁；

求小李参加考核的次数

已知函数f(x)＝sin()(＞0，0≤≤π)为偶函数，且其图像上相邻的一个最高点和最低点之间距离为．

求f(x)的解析式；

若tanα＋cotα＝5，求的值．

设aR，函数f(x)＝3x³－4x＋a＋1．

(Ⅰ)求f(x)的单调区间；

(Ⅱ)若对于任意x[－2，0]，不等式f(x)≤0恒成立，求a的最大值；

(Ⅲ)若方程f(x)＝0存在三个相异的实数根，求a的取值范围．

已知抛物线的方程为x²＝2y，F是抛物线的焦点，过点F的直线l与抛物线相交于A、B两点，分别过点A、B作抛物线的两条切线l₁和l₂，记l₁和l₂相交于点M．

(Ⅰ)证明：l₁⊥l₂；

(Ⅱ)求点M的轨迹方程．

在数列{a_n}中，a₁＝3，a_n＝－a_n－1－2_n+1(n≥2，且nN*)．

(Ⅰ)求a₂，a₃的值；

(Ⅱ)证明：数列{a_n＋n}是等比数列，并求{a_n}的通项公式；

(Ⅲ)求数列{a_n}的前n项和S_n．

如图，在正四棱柱ABCD-A₁B₁C₁D₁中，AA₁＝，AB＝l，E是DD₁的中点．

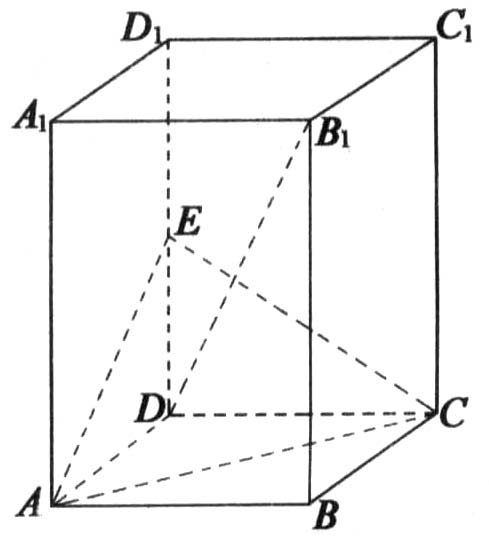
(Ⅰ)求证：AC⊥B_lD；

(Ⅱ)求二面角E－AC－B的大小．

设甲，乙两人每次投球命中的概率分别是，，且两人各次投球是否命中相互之间没有影响．

(Ⅰ)若两人各投球1次，求两人均没有命中的概率；

(Ⅱ)若两人各投球2次，求乙恰好比甲多命中1次的概率．

已知函数f(x)＝e^x－x(e为自然对数的底数)．

(Ⅰ)求f(x)的最小值；

(Ⅱ)设不等式f(x)＞－ax的解集为P，且{x|0≤}x≤2}P，求实数a的取值范围；

(Ⅲ)设nN*，证明：＜．

已知抛物线的方程为x²＝2py(p＞0)，过点p(0，p)的直线l与抛物线相交于A、B两点，分别过点A、B作抛物线的两条切线l₁和l₂，记l₁和l₂相交于点M．

(Ⅰ)证明：直线l₁和l₂的斜率之积为定值；

(Ⅱ)求点M的轨迹方程．

某项竞赛分为初赛、复赛、决赛三个阶段进行，每个阶段选手要回答一个问题，规定正确回答问题者进入下一阶段竞赛，否则即遭淘汰．已知某选手通过初赛、复赛、决赛的概率分别是，，，且各阶段通过与否相互独立．

(Ⅰ)求该选手在复赛阶段被淘汰的概率；

(Ⅱ)设该选手在竞赛中回答问题的个数为ξ，求ξ的数学期望和方差．