已知函数f(x)＝a·lnx＋b·x²在点(1，f(1))处的切线方程为x－y－1＝0．

(1)求f(x)的表达式；

(2)若f(x)满足f(x)≥g(x)恒成立，则称f(x)是g(x)的一个“上界函数”，如果函数f(x)为g(x)＝－lnx(t为实数)的一个“上界函数”，求t的取值范围；

(3)当m＞0时，讨论F(x)＝f(x)＋－x在区间(0，2)上极值点的个数．

已知二次函数h(x)＝ax²＋bx＋c(其中c＜3)，其导函数y＝(x)的图象如图，f(x)＝6lnx＋h(x)．

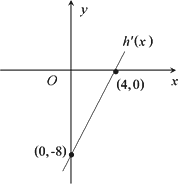
(1)求函数f(x)在x＝3处的切线斜率；

(2)若函数y＝－x，x∈(0，6]的图像总在函数y＝f(x)图象的上方，求c的取值范围．

已知函数f(x)＝ax³＋bx²－3x在x＝±1处取得极值．

(1)求函数f(x)的解析式；

(2)求证：对于区间[－1，1]上任意两个自变量的值x₁，x₂，都有|f(x₁)－f(x₂)|≤4；

(3)若过点A(1，m)(m≠－2)可作曲线y＝f(x)的三条切线，求实数m的取值范围．

已知函数f(x)＝x³＋mx²＋nx－2的图象过点(－1，－6)，且函数g(x)＝(x)＋6x是偶函数．

(Ⅰ)求m、n的值；

(Ⅱ)若a＞0，求函数y＝f(x)在区间(a－1，a＋1)内的极值．

某企业生产一种产品时，固定成本为5000元，而每生产100台产品时直接消耗成本要增加2500元，市场对此商品年需求量为500台，销售的收入函数为(万元)(0≤x≤5)，其中x是产品售出的数量(单位：百台)

(1)把利润表示为年产量的函数；

(2)年产量多少时，企业所得的利润最大；

某工厂每天生产某种产品最多不超过40件，并且在生产过程中产品的正品率P与每日生产产品件数x(x∈N^*)间的关系为，每生产一件正品盈利4000元，每出现一件次品亏损2000元．(注：正品率＝产品的正品件数÷产品总件数×100％)

(Ⅰ)将日利润y(元)表示成日产量x(件)的函数；

(Ⅱ)求该厂的日产量为多少件时，日利润最大？并求出日利润的最大值．

已知函数f(x)＝x³－ax²＋(a²－1)x＋b(a，b∈R)，其图象在点(1，f(1))处的切线方程为x＋y－3＝0．

(1)求a，b的值；

(2)求函数f(x)的单调区间，并求出f(x)在区间[－2，4]上的最大值．

已知函数f(x)＝．

(1)若f(x)在x∈[1，＋∞)上有零点，求实数a的取值范围；

(2)若f(x)在x∈[1，＋∞)上单调递增，求实数a的取值范围．

某地发生特大地震和海啸，使当地的自来水受到了污染，某部门对水质检测后，决定往水中投放一种药剂来净化水质．已知每投放质量为m的药剂后，经过x天该药剂在水中释放的浓度y(毫克/升)满足，当药剂在水中释放的浓度不低于4(毫克/升)时称为有效净化；当药剂在水口释放的浓度不低于4(毫克/升)且不高于10(毫克/升)时称为最佳净化．

(Ⅰ)如果投放的药剂质量为m＝4，试问自来水达到有效净化一共可持续几天？

(Ⅱ)如果投放的药剂质量为m，为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化，试确定该投放的药剂质量m的值．

已知函数f(x)＝－x³＋ax²＋bx＋c在(－∞，0)上是减函数，在(0，1)上是增函数，函数f(x)在R上有三个零点，且1是其中一个零点．

(Ⅰ)求实数b的值；

(Ⅱ)求实数a的取值范围．