如图，在底面是正方形的四棱锥P－ABCD中，PA⊥面ABCD，BD交AC于点E，F是PC中点，G为AC上一点．

(1)求证：BD⊥FG；

(2)确定点G在线段AC上的位置，使FG∥平面PBD，并说明理由．

(3)当二面角B－PC－D的大小为时，求PC与底面ABCD所成角的正切值．

已知点P是直角坐标平面内的动点，点P到直线(p是正常数)的距离为d₁，到点的距离为d₂，且d₁－d₂＝1．

(1)求动点P所在曲线C的方程；

(2)直线l过点F且与曲线C交于不同两点A、B，分别过A、B点作直线的垂线，对应的垂足分别为M、N，求证＝0；

(3)记，，(A、B、M、N是(2)中的点)，，求λ的值．

已知等差数列满足a₁＝1，a₃＝6，若对任意的n∈N^*，数列{b_n}满足b_n，2a_n+1，b_n+1依次成等比数列，且b₁＝4．

(Ⅰ)求a_n，b_n

(Ⅱ)设，证明：对任意的n∈N^*，

设函数f(x)＝x³―ax²―ax，g(x)＝2x²＋4x＋c．

(1)试问函数f(x)能否在x＝－1时取得极值？说明理由；

(2)若a＝－1，当x∈[－3，4]时，函数f(x)与g(x)的图像有两个公共点，求c的取值范围．

某种产品的广告费支出x与销售额y(单位：万元)之间有如下对应数据：

(Ⅰ)求回归直线方程；

(Ⅱ)试预测广告费支出为10万元时，销售额多大？

(Ⅲ)在已有的五组数据中任意抽取两组，求至少有一组数据其预测值与实际值之差的绝对值不超过5的概率．

(参考数据：，参考公式：回归直线方程y＝a＋bx，其中)

如图甲，在平面四边形ABCD中，已知∠A＝45°，∠C＝90°，∠ADC＝105°，AB＝BD，现将四边形ABCD沿BD折起，使平面ABD⊥平面BDC(如图乙)，设点E、F分别为棱AC、AD的中点．

(Ⅰ)求证：DC⊥平面ABC；

(Ⅱ)设CD＝a，求三棱锥A－BFE的体积．

已知向量＝(1，cosx)，＝(sinx，)(＞0)，函数f(x)＝·，且f(x)图象上一个最高点的坐标为(，2)，与之相邻的一个最低点的坐标为(，－2)．

(1)求f(x)的解析式；

(2)在△ABC中，a，b，c是角A、B、C所对的边，且满足a²＋c²－b²＝ac，求角B的大小以及f(A)的取值范围．

已知函数f(x)＝ax²－2x＋lnx．

(1)若f(x)无极值点，但其导函数f(x)有零点，求a的值；

(2)若f(x)有两个极值点，求a的取值范围，并证明f(x)的极小值小于．

已知A，B分别为曲线与x轴的左、右两个交点，直线l过点B且与x轴垂直，P为l上异于点B的点，连结AP与曲线C交于点M．

(1)若曲线C为圆，M为圆弧的三等分点，试求点P的坐标；

(2)设N是以BP为直径的圆与线段BM的交点，若O，N，P三点共线，求a的值．

三棱锥A－BCD中，平面ABD⊥平面ACD，，，∠CAD＝30°．

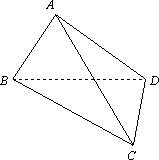
(1)求证：AB⊥CD；

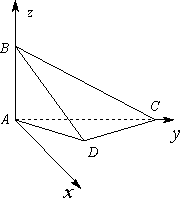
(2)建立如图直角坐标系，使AB在z轴上，AC在y轴上试写出点D的坐标，并求二面角A―BC―D的余弦值．