如图1，∠ACB＝45°，BC＝3，过动点A作AD⊥BC，垂足D在线段BC上且异于点B，连接AB，沿AD将△ABD折起，使∠BDC＝90(如图2所示)．

(Ⅰ)当BD的长为多少时，三棱锥A－BCD的体积最大；

(Ⅱ)当三棱锥A＝BCD的体积最大时，设点E，M分别为棱BC，AC的中点，试在棱CD上确定一点N，使得EN⊥BM，并求EN与平面BMN所成角的大小．

已知等差数列{a_n}前三项的和为－3，前三项的积为8．

(Ⅰ)求等差数列{a_n}的通项公式；

(Ⅱ)若a₂，a₃，a₁成等比数列，求数列{|a_n|}的前n项和．

已知向量a＝(cosωx－sinωx，sinωx)，b＝(－cosωx－sinωx，2cosωx)，设函数f(x)＝a·b＋λ(x∈R)的图象关于直线x＝π对称，其中ω，λ为常数，且ω∈(，1)．

(Ⅰ)求函数f(x)的最小正周期；

(Ⅱ)若y＝f(x)的图象经过点(，0)，求函数f(x)在区间[0，]上的取值范围．

数列{x_n}满足：x₁＝0，x_n+1＝－x＋x_n＋c(n∈N^*)

(1)证明：数列{x_n}是单调递减数列的充分必要条件是c＜0

(2)求c的取值范围，使数列{x_n}是单调递增数列．

如图，F₁(－c，0)，F₂(c，0)分别是椭圆的左，右焦点，过点F₁作x轴的垂线交椭圆的上半部分于点P，过点F₂作直线PF₂的垂线交直线x＝于点Q；

(1)若点Q的坐标为(4，4)；求椭圆C的方程；

(2)证明：直线PQ与椭圆C只有一个交点．

设f(x)＝ae^x＋＋b(b＞0)

(1)求f(x)在[0，＋∞)上的最小值；

(2)设曲线y＝f(x)在点(2，f(2))的切线方程为y＝x；求a，b的值．

平面图形ABB₁A₁C₁C如下图1所示，其中BB₁C₁C是矩形，BC＝2，BB₁＝4，AB＝AC＝，A₁B₁＝A₁C₁＝．现将该平面图形分别沿BC和B₁C₁折叠，使ΔABC与ΔA₁B₁C₁所在平面都与平面BB₁C₁C垂直，再分别连接AA₁，BA₁，CA₁，得到如下图2所示的空间图形，对此空间图形解答下列问题．

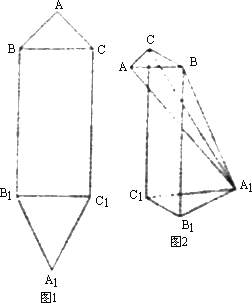
(Ⅰ)证明：AA₁⊥BC；

(Ⅱ)求AA₁的长；

(Ⅲ)求二面角A－BC－A₁的余弦值．

某单位招聘面试，每次从试题库随机调用一道试题，若调用的是A类型试题，则使用后该试题回库，并增补一道A类试题和一道B类型试题入库，此次调题工作结束；若调用的是B类型试题，则使用后该试题回库，此次调题工作结束．试题库中现共有n＋m道试题，其中有n道A类型试题和m道B类型试题，以X表示两次调题工作完成后，试题库中A类试题的数量．

(Ⅰ)求X＝n＋2的概率；

(Ⅱ)设m＝n，求X的分布列和均值(数学期望)．

设函数

(1)求函数f(x)的最小正周期；

(2)设函数g(x)对任意x∈R，有，且当时，；求函数g(x)在[－π，0]上的解析式．

已知以原点O为中心的椭圆，它的短轴长为，右焦点F(c，0)(c＞0)，它的长轴长为2a(a＞c＞0)，直线与x轴相交于点A，|OF|＝2|FA|，过点A的直线与椭圆相交于P、Q两点．

(Ⅰ)求椭圆的方程和离心率；

(Ⅱ)若·＝0，求直线PQ的方程；

(Ⅲ)设＝λ(λ＞1)，过点P且平行于直线l的直线与椭圆相交于另一点M，证明：＝－λ．