巳知二次函数f(x)＝ax²＋bx＋c和g(x)＝ax²＋bx＋c·lnx(abc≠0)．

(Ⅰ)证明：当a＜0时，无论b为何值，函数g(x)在定义域内不可能总为增函数；

(Ⅱ)在同一函数图象上取任意两个不同的点A(x₁，y₁)，B(x₂，y₂)，线段AB的中点C(x₀，y₀)，记直线AB的斜率为k若f(x)满足k＝(x₀)，则称其为"K函数”．判断函数f(x)＝ax²＋bx＋c与g(x)＝ax²＋bx＋c·lnx(abc≠0)是否为"K函数”？并证明你的结论．

巳知椭圆M：(a＞b＞0)的长轴长为4，且与椭圆有相同的离心率．

(Ⅰ)求椭圆M的方程；

(Ⅱ)是否存在圆心在原点的圆，使得该圆的任意一条切线与M有两个交点A、B，且⊥？若存在，写出该圆的方程，并求|AB|的取值范围，若不存在，说明理由．

如图，有一块边长为1 km的正方形区域ABCD，在点A处有一个可转动的探照灯，其照射角∠PAQ始终为45°(其中点P，Q分别在边BC，CD上)，设∠PAB＝，tan＝t

(Ⅰ)用t表示出PQ的长度，并探求△CPQ的周长l是否为定值．

(Ⅱ)问探照灯照射在正方形ABCD内部区域的面积S的最大值是多少(km²)？

如图，在多面体ABCDE中，DB丄平面ABC，AE∥DB，且△ABC是边长为2的等边三角形，AE＝1，BD＝2．

(Ⅰ)在线段DC上存在一点F，使得EF丄面DBC，试确定F的位置，并证明你的结论；

(Ⅱ)求二面角D－EC－B的平面角的余弦值．

随机调查某社区80个人，以研究这一社区居民在20∶00－22∶00时间段的休闲方式与性别的关系，得到下面的数据表：

(Ⅰ)在该社区随机调查3名男性(以所抽取样本的频率估计为总体的概率)，设调查的3人在这一时间段以看书为休闲方式的人数为随机变量X，求X的分布列和期望；

(Ⅱ)根据以上数据，能否有99％的把握认为“在20∶00－22∶00时间段的休闲方式与性别有关系？

参考公式：K²＝，其中n＝a＋b＋c＋d．

巳知向量m＝(sin，1)，n＝(cos，cos²)，f(x)＝m·n

(Ⅰ)若f(x)＝1，求cos(＋x)的值；

(Ⅱ)在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cosB＝bcosC，求函数f(A)的取值范围．

已知函数f(x)＝ax＋lnx，a∈R

(Ⅰ)求函数f(x)的单调区间；

(Ⅱ)是否存在实数a，使不等式f(x)＜ax²对x∈(1，＋∞)恒成立，若存在，求实数a的取值范围，若不存在，请说明理由．

已知平面内一动点P到点F(1，0)的距离等于它到直线x＝－1的距离．

(Ⅰ)求动点P的轨迹C的方程；

(Ⅱ)若直线l与曲线C交于P、Q两点，且·＝0，又点E(－1，0)，求·的最小值．

如图，某市拟在长为4 km的道路OP的一侧修建一条运动赛道，赛道的前一部分为曲线段OSM，该曲线段为函数y＝Asinωx(A＞0，ω＞0)，x∈[0，2]的图象，且图象的最高点为S(，)；赛道的后一部分为折线段MNP，为保证参赛运动员的安全，限定∠MNP＝120°．

(Ⅰ)求A，ω的值和M，P两点间的距离；

(Ⅱ)应如何设计，才能使折线段赛道MNP最长？

如图所示，三棱柱ABC－A₁B₁C₁中，AB＝AC＝AA₁＝2，平面ABC₁⊥平面A₁ACC₁，又∠AA₁C₁＝∠BAC₁＝60°，AC₁与A₁C相交于点O．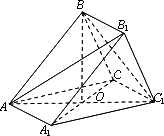

(Ⅰ)求证：BO⊥平面A₁ACC₁；

(Ⅱ)求AB₁与平面A₁ACC₁所成角的正弦值；