已知斜三棱柱ABC-A1B1C1的底面是直角三角形.∠ACB=90°.侧棱与底面所成角为θ.点B1在底面上的射影D落在BC上.(1)求证:AC⊥平面BB1C1C,(2)若.且当AC=BC=AA1=3时——青夏教育精英家教网—

相关习题

0 22053 22061 22067 22071 22077 22079 22083 22089 22091 22097 22103 22107 22109 22113 22119 22121 22127 22131 22133 22137 22139 22143 22145 22147 22148 22149 22151 22152 22153 22155 22157 22161 22163 22167 22169 22173 22179 22181 22187 22191 22193 22197 22203 22209 22211 22217 22221 22223 22229 22233 22239 22247 266669

科目： 来源：广东省模拟题 题型：解答题

已知斜三棱柱ABC-A₁B₁C₁的底面是直角三角形，∠ACB=90°，侧棱与底面所成角为θ，点B₁在底面上的射影D落在BC上，
（1）求证：AC⊥平面BB₁C₁C；
（2）若

，且当AC=BC=AA₁=3时，求二面角C-AB-C₁的大小。

查看答案和解析>>

科目： 来源：浙江省期末题 题型：解答题

如图，已知△AOB，∠AOB=

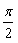，∠BAO=

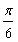，AB=4，D为线段AB的中点。若△AOC是△AOB绕直线AO旋转而成的，记二面角B-AO-C的大小为θ。
(1)当平面COD⊥平面AOB时，求θ的值；
(2)当θ∈[

，

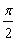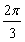]时，求二面角C-OD-B的余弦值的取值范围．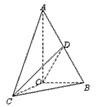

查看答案和解析>>

科目： 来源：0110 月考题 题型：解答题

如图，直三棱柱A₁B₁C₁-ABC中，C₁C=CB=CA=2，AC⊥CB，D、E分别为棱C₁C、B₁C₁的中点。
（1）求点E到平面ADB的距离；
（2）求二面角E-A₁D-B的平面角的余弦值；
（3）在线段AC上是否存在一点F，使得EF⊥平面A₁DB？若存在，确定其位置；若不存在，说明理由。

查看答案和解析>>

科目： 来源：广东省月考题 题型：解答题

如图，已知矩形ABCD的边AB=2 ，BC=，点E、F分别是边AB、CD的中点，沿AF、EC分别把三角形ADF和三角形EBC折起，使得点D和点B重合，记重合后的位置为点P。
（1）求证：平面PCE⊥平面PCF；
（2）设M、N分别为棱PA、EC的中点，求直线MN与平面PAE所成角的正弦；
（3）求二面角A-PE-C的大小。