
科目: 来源: 题型:
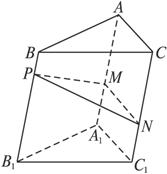
(1)求证:CC1⊥MN;
(2)在任意△DEF中有余弦定理:DE2=DF2+EF2-2DF·EFcos∠DFE.拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明.
查看答案和解析>>
科目: 来源: 题型:

查看答案和解析>>
科目: 来源: 题型:
(1)设A在SB、SP上的射影分别为H、N,求证:AN⊥平面SPB;
(2)证明∠AHN是二面角ASBP的平面角;
(3)若∠ASB=60°,∠PAB=α,∠AHN=β,求证:tanαtanβ=2.

查看答案和解析>>
科目: 来源: 题型:
(1)当a为何值时,BD⊥平面PAC?试证明你的结论.
(2)当a=4时,求证:BC边上存在一点M,使得PM⊥DM.
(3)若在BC边上至少存在一点M,使PM⊥DM,求a的取值范围.
查看答案和解析>>
科目: 来源: 题型:
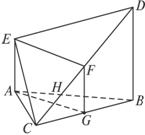
(1)求证:EF⊥平面BCD;
(2)求多面体ACBDE的体积.
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
科目: 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com