
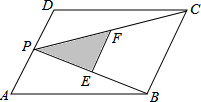
 如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )
如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1,S2.若S=3,则S1+S2的值为( )| A. | 24 | B. | 12 | C. | 6 | D. | 3 |
分析 过P作PQ平行于DC,由DC与AB平行,得到PQ平行于AB,可得出四边形PQCD与ABQP都为平行四边形,进而确定出△PDC与△PCQ面积相等,△PQB与△ABP面积相等,再由EF为△BPC的中位线,利用中位线定理得到EF为BC的一半,且EF平行于BC,得出△PEF与△PBC相似,相似比为1:2,面积之比为1:4,求出△PBC的面积,而△PBC面积=△CPQ面积+△PBQ面积,即为△PDC面积+△PAB面积,即为平行四边形面积的一半,即可求出所求的面积.
解答 解:过P作PQ∥DC交BC于点Q,由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP,S△ABP=S△QPB,
∵EF为△PCB的中位线,
∴EF∥BC,EF=$\frac{1}{2}$BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=3,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=12.
故选:B.
点评 此题考查了平行四边形的性质,相似三角形的判定与性质,熟练掌握平行四边形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
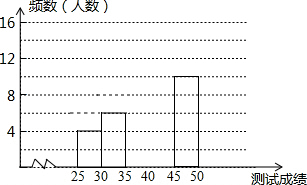 为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:| 组别 | 成绩x分 | 频数(人数) |
| 第1组 | 25≤x<30 | 4 |
| 第2组 | 30≤x<35 | 6 |
| 第3组 | 35≤x<40 | 14 |
| 第4组 | 40≤x<45 | a |
| 第5组 | 45≤x<50 | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com