
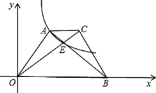
【题目】如图,梯形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点,若AC : OB = 1:3,梯形AOBC面积为24,则k =( )
(k>0)经过A、E两点,若AC : OB = 1:3,梯形AOBC面积为24,则k =( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
设△ACE的面积为S,则可得出△BOE的面积为9S,△AOE的面积为3S,△CEB的面积为3S,从而求出S.过点E作EF⊥OB,过点A作AM⊥OB于点M,设△OAM的面积为a,则△OEF的面积也为a,利用△BEF∽△BAM可得出a的值,即△OEF的面积,则可求出k的值.
解:∵四边形AOBC是梯形,AC∥OB,AC:OB=1:3,
∴CE:EO=1:3,AE:EB=1:3,
设△ACE的面积为S,则△BOE的面积为9S,△AOE的面积为3S,△CEB的面积为3S,
又∵梯形AOBC面积为24,
∴S+9S+3S+3S=24,
解得S=![]() .
.
过点E作EF⊥OB,过点A作AM⊥OB于点M,

设△OAM的面积为a,则△OEF的面积也为a,则△AMB的面积=18-a,△EFB的面积为![]() .
.
∵EF∥AM,
∴△AMB∽△EFB,
∴![]() ,
,
解得a=![]() ,则k=
,则k=![]() ,
,
故选择C.


科目:初中数学 来源: 题型:
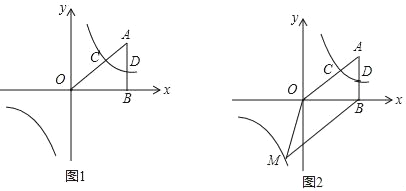
【题目】如图1,在平面直角坐标系中,A点的坐标为(m,3),AB⊥x轴于点B,tan∠OAB=![]() ,反比例函数y1=
,反比例函数y1=![]() 的图象的一支经过AO的中点C,且与AB交于点D.
的图象的一支经过AO的中点C,且与AB交于点D.
(1)求反比例函数解析式;
(2)设直线OA的解析式为y2=nx,请直接写出y1<y2时,自变量x的取值范围 .
(3)如图2,若函数y=3x与y1=![]() 的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.
的图象的另一支交于点M,求△OMB与四边形OCDB的面积的比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
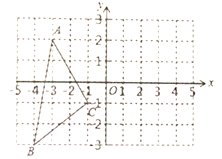
【题目】如图,(1)在网格中画出![]() 关于y轴对称的
关于y轴对称的![]() ;
;
(2)在y轴上确定一点P,使![]() 周长最短,(只需作图,保留作图痕迹)
周长最短,(只需作图,保留作图痕迹)
(3)写出![]() 关于x轴对称的
关于x轴对称的![]() 的各顶点坐标;
的各顶点坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某部门组织调运一批物资,一运送物资车开往距离出发地180千米的目的地,出发第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地.设原计划速度为x千米/小时,则方程可列为( )
A. ![]() +
+![]() =
=![]() B.
B. ![]() -
-![]() =
=![]() C.
C. ![]() +1=
+1=![]() ﹣
﹣![]() D.
D. ![]() +1=
+1=![]() +
+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】过正方形![]() (四边都相等,四个角都是直角)的顶点
(四边都相等,四个角都是直角)的顶点![]() 作一条直线
作一条直线![]() .
.
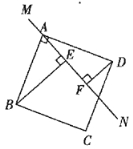
图(1) 图(2) 图(3)
(1)当![]() 不与正方形任何一边相交时,过点
不与正方形任何一边相交时,过点![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() 如图(1),请写出
如图(1),请写出![]() ,
,![]() ,
,![]() 之间的数量关系,并证明你的结论.
之间的数量关系,并证明你的结论.
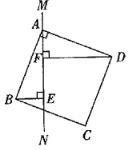
(2)若改变直线![]() 的位置,使
的位置,使![]() 与
与![]() 边相交如图(2),其它条件不变,
边相交如图(2),其它条件不变,![]() ,
,![]() ,
,![]() 的关系会发生变化,请直接写出
的关系会发生变化,请直接写出![]() ,
,![]() ,
,![]() 的数量关系,不必证明;
的数量关系,不必证明;
(3)若继续改变直线![]() 的位置,使
的位置,使![]() 与
与![]() 边相交如图(3),其它条件不变,
边相交如图(3),其它条件不变,![]() ,
,![]() ,
,![]() 的关系又会发生变化,请直接写出
的关系又会发生变化,请直接写出![]() ,
,![]() ,
,![]() 的数量关系,不必证明.
的数量关系,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与直线
与直线![]() 交于点A,点A的横坐标为
交于点A,点A的横坐标为![]() ,且直线
,且直线![]() 与x轴交于点B,与y轴交于点D,直线
与x轴交于点B,与y轴交于点D,直线![]() 与y轴交于点C.
与y轴交于点C.
(1)求点A的坐标及直线![]() 的函数表达式;
的函数表达式;
(2)连接![]() ,求
,求![]() 的面积.
的面积.
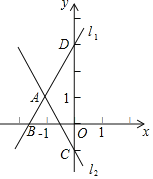
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图直线![]() 对应的函数表达式为
对应的函数表达式为![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .直线
.直线![]() :
:![]() 与
与![]() 轴交于点
轴交于点![]() ,且经过点
,且经过点![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() .
.
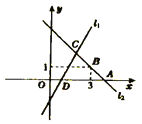
(1)求点![]() ,点
,点![]() 的坐标;
的坐标;
(2)求直线![]() 对应的函数表达式;
对应的函数表达式;
(3)求![]() 的面积;
的面积;
(4)利用函数图象写出关于![]() ,
,![]() 的二元一次方程组
的二元一次方程组![]() 的解.
的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=72°,BD、CE分别是△ABC、△BCD的角平分线.则图中的等腰三角形有( )

A.5个B.4个C.3个D.2个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com