
| 时间x(天) | 1≤x≤40 | 40≤x≤70 |
| 售价(元/件) | x+45 | 85 |
| 每天销售(件) | 150-2x | |
分析 (1)根据单价乘以数量,可得利润,可得答案;
(2)根据分段函数的性质,可分别得出最大值,根据有理数的比较,可得答案;
(3)根据二次函数值大于或等于3250,一次函数值大于或等于3250,可得不等式,根据解不等式组,可得答案.
解答 解:(1)当1≤x<40时,y=(150-2x)(x+45-30)=-2x2+120x+2250,
当40≤x≤70时,y=(150-2x)(85-30)=-110x+8250,
综上所述:y=$\left\{\begin{array}{l}{-2{x}^{2}+120x+2250(1≤x<40)}\\{-110x+8250(40≤x≤70)}\end{array}\right.$;
(2)当1≤x<40时,二次函数开口向下,二次函数对称轴为x=30,
当x=30时,y最大=-2×302+120×30+2250=4050,
当40≤x≤70时,y随x的增大而减小,
当x=40时,y最大=3850,
综上所述,该商品第30天时,当天销售利润最大,最大利润是4050元;
(3)当1≤x<40时,y=-2x2+120x+2250≥3250,解得10≤x≤50,
因此利润不低于3250元的天数是10≤x<40,共30天;
当40≤x≤70时,y=-110x+8250≥3250,解得x≤45$\frac{5}{11}$,
因此利润不低于3250元的天数是40≤x≤45,共6天,
所以该商品在销售过程中,共36天每天销售利润不低于3250元.
点评 本题考查了二次函数的应用,利用单价乘以数量求函数解析式,利用了函数的性质求最值.


科目:初中数学 来源: 题型:解答题
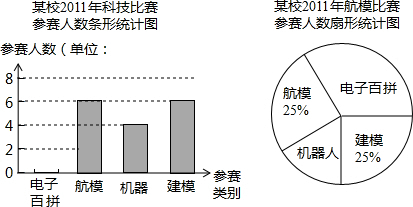
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 2 | C. | 1 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{36}$ | C. | $\sqrt{\frac{a}{b}}$ | D. | $\sqrt{a+4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
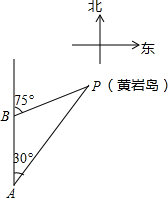 如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)
如图,三沙市一艘海监船某天在黄岩岛P附近海域由南向北巡航,某一时刻航行到A处,测得该岛在北偏东30°方向,海监船以20海里/时的速度继续航行,2小时后到达B处,测得该岛在北偏东75°方向,求此时海监船与黄岩岛P的距离BP的长.(参考数据:$\sqrt{2}$≈1.414,结果精确到0.1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 原价 | 每个房间增加10元 | 每个房间增加20元 | … | 每个房间增加10x元 | |
| 每个房价定价 | 180 | 190 | 200 | … | |
| 房住房间数量 | 50 | 49 | 48 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
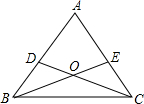 如图,已知△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.
如图,已知△ABC中,AB=AC,点D、E分别在AB、AC上,且BD=CE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com