
【题目】如图,在![]() 中,
中,![]() ,且
,且![]() ,
,![]() ,
,![]() 为
为![]() 的中点,
的中点,![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() .
.
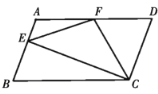
(1)求证:![]() ;
;
(2)当![]() 为何值时,
为何值时,![]() 的值最大?并求此时
的值最大?并求此时![]() 的值.
的值.
【答案】(1)见解析;(2)![]() 时,
时,![]() 的值最大,
的值最大,![]()
【解析】
(1)延长BA、CF交于点G,利用可证△AFG≌△DFC得出![]() ,
,![]() ,根据
,根据![]() ,可证出
,可证出![]() ,得出
,得出![]() ,利用
,利用![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,得出
的中点,得出![]() ,
,![]() ,则有
,则有![]() ,可得出
,可得出![]() ,得出
,得出![]() ,即可得出结论;
,即可得出结论;
(2)设BE=x,则![]() ,
,![]() ,由勾股定理得出
,由勾股定理得出![]() ,
,![]() ,得出
,得出![]() ,求出
,求出![]() ,由二次函数的性质得出当x=1,即BE=1时,CE2-CF2有最大值,
,由二次函数的性质得出当x=1,即BE=1时,CE2-CF2有最大值,![]() ,由三角函数定义即可得出结果.
,由三角函数定义即可得出结果.
解:(1)证明:如图,延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
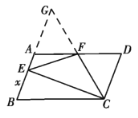
∵![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
在![]() 中,
中,![]() ,
,
∴![]() .
.
在![]() 和
和![]() 中,
中,
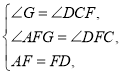
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() .
.
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,
的中点,
∴![]() ,
,![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
在![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() .
.
∴![]()
(2)设![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴当![]() ,即
,即![]() 时,
时,![]() 的值最大,
的值最大,
∴![]() .
.
在![]() 中,
中,![]()


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
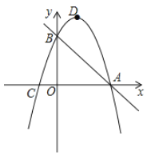
【题目】已知,如图,抛物线![]() 经过直线
经过直线![]() 与坐标轴的两个交点
与坐标轴的两个交点![]() .此抛物线与
.此抛物线与![]() 轴的另一个交点为
轴的另一个交点为![]() .抛物线的顶点为
.抛物线的顶点为![]() .
.
![]() 求此抛物线的解析式;
求此抛物线的解析式;
![]() 若点
若点![]() 为抛物线上一动点,是否存在点
为抛物线上一动点,是否存在点![]() .使
.使![]() 与
与![]() 的面积相等?若存在,求点
的面积相等?若存在,求点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
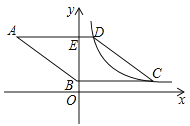
【题目】如图,菱形![]() 的边
的边![]() 轴,垂足为点
轴,垂足为点![]() ,顶点
,顶点![]() 在第二象限,顶点
在第二象限,顶点![]() 在
在![]() 轴的正半轴上,反比例函数
轴的正半轴上,反比例函数![]() (
(![]() ,
,![]() )的图象同时经过顶点
)的图象同时经过顶点![]() ,
,![]() ,若点
,若点![]() 的横坐标为10,
的横坐标为10,![]() ,则
,则![]() 的值为_______.
的值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知点A,B,C是⊙O上的三点,以AB,BC为邻边作ABCD,延长AD,交⊙O于点E,过点A作CE的平行线,交CD的延长线于F.
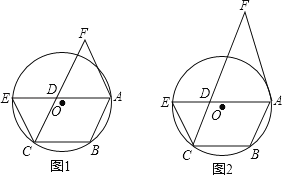
(1)求证:FD=FA;
(2)如图2,连接AC,若∠F=40°,且AF恰好是⊙O的切线,求∠CAB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 与
与 ![]() 轴交于
轴交于![]() 和
和![]() ,与
,与 ![]() 轴交于
轴交于 ![]() 点,点
点,点![]() 关于抛物线的对称轴的对称点为点
关于抛物线的对称轴的对称点为点![]() .
.
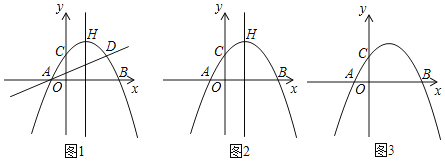
(1)求此抛物线的解析式和对称轴.
(2)如图 2,当点![]() 在抛物线的对称轴上运动时,在直线
在抛物线的对称轴上运动时,在直线![]() 上是否存在点
上是否存在点![]() ,使得以点
,使得以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形为平行四边形?若存在,请求出点
为顶点的四边形为平行四边形?若存在,请求出点 ![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
(3)如图 3,当点![]() 、
、![]() 、
、![]() 三点共圆时,请求出该圆圆心的坐标.
三点共圆时,请求出该圆圆心的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是边长为1的正方形ABCD的对角线,BE平分∠DBC交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G.
(1)求证:△BCE≌△DCF;
(2)求CF的长。

查看答案和解析>>
科目:初中数学 来源: 题型:
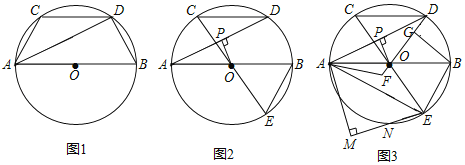
【题目】如图,在⊙O中,AB是⊙O的直径,CD∥AB,
(1)如图1,证明:AC=BD;
(2)如图2,连接CO并延长交⊙O于点E,OP⊥AD,垂足为P,证明:BE=2OP;
(3)如图3,在(2)的条件下,连接DO,点F为DO延长线上一点,若∠AFO+∠ABE=180°,过点B作BG⊥OD,垂足为G,点N为![]() 上一点,AM⊥EN,垂足为M,若GF=4,OP=
上一点,AM⊥EN,垂足为M,若GF=4,OP=![]() ,AM=2NE,求AM的长.
,AM=2NE,求AM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“2017年张学友演唱会”于6月3日在我市关山湖奥体中心举办,小张去离家2520米的奥体中心看演唱会,到奥体中心后,发现演唱会门票忘带了,此时离演唱会开始还有23分钟,于是他跑步回家,拿到票后立刻找到一辆“共享单车”原路赶回奥体中心,已知小张骑车的时间比跑步的时间少用了4分钟,且骑车的平均速度是跑步的平均速度的1.5倍.
(1)求小张跑步的平均速度;
(2)如果小张在家取票和寻找“共享单车”共用了5分钟,他能否在演唱会开始前赶到奥体中心?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“赏中华诗词,寻文化基因,品生活之美”,某校举办了首届“中国诗词大会”,经选拔后有50名学生参加决赛,这50名学生同时默写50首古诗词,若每正确默写出一首古诗词得2分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表.
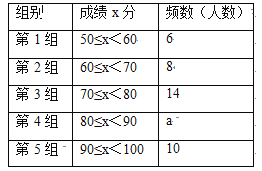
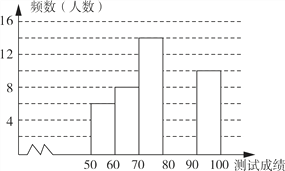
请结合图表完成下列各题:
(1)① 表中a的值为 ;
② 把频数分布直方图补充完整;
(2)若测试成绩不低于80分为优秀,则本次测试的优秀率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com