
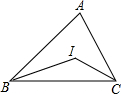
 如图,BI,CI分别平分∠ABC,∠ACB,若BAC=70°,则∠BIC=( )
如图,BI,CI分别平分∠ABC,∠ACB,若BAC=70°,则∠BIC=( )| A. | 140° | B. | 110° | C. | 125° | D. | 105° |
分析 求出∠ABC+∠ACB度数,根据角平分线求出∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB)=55°,根据三角形内角和定理求出即可.
解答 解:∵∠A=70°,
∴∠ABC+∠ACB=180°-70°=110°,
∵BI、CI分别平分∠ABC,∠ACB,
∴∠IBC=$\frac{1}{2}$∠ABC,∠ICB=$\frac{1}{2}$∠ACB,
∴∠IBC+∠ICB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×110°=55°,
∴∠BIC=180°-(∠IBC+∠ICB)=180°-55°=125°.
故选:C.
点评 本题考查了三角形内角和定理和角平分线定义的应用,注意掌握:三角形的内角和等于180°.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{8a}$ | B. | $\sqrt{{a}^{2}+{b}^{2}}$ | C. | $\sqrt{0.1x}$ | D. | $\sqrt{{a}^{5}}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 若两条直线被第三条直线所截,则同旁内角互补 | |
| B. | 相等的角是对顶角 | |
| C. | 三角形的外角等于两个内角的和 | |
| D. | 若三条直线两两相交,则共有6对对顶角 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
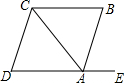 如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )
如图,点E在DA的延长线上,下列条件中能判定AB∥CD的是( )| A. | ∠B=∠BAE | B. | ∠BCA=∠CAD | C. | ∠BCA+∠CAE=180° | D. | ∠D=∠BAE |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com