
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:解答题
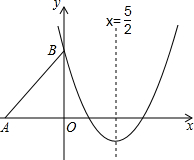 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
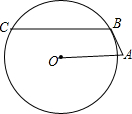 如图,AB切⊙O于点B,OA=2$\sqrt{3}$,∠BAO=60°,弦BC∥OA,则$\widehat{BC}$的长为2π(结果保留π).
如图,AB切⊙O于点B,OA=2$\sqrt{3}$,∠BAO=60°,弦BC∥OA,则$\widehat{BC}$的长为2π(结果保留π).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
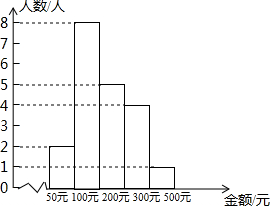 某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论正确的是( )
某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论正确的是( )| A. | 样本中位数是200元 | |
| B. | 样本容量是20 | |
| C. | 该企业员工捐款金额的极差是450元 | |
| D. | 该企业员工最大捐款金额是500元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
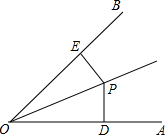 如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )
如图,∠POA=∠POB,PD⊥OA于点D,PE⊥OB于点E,若OP=26,PE=10,则OD的长为( )| A. | 12 | B. | 18 | C. | 20 | D. | 24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com