
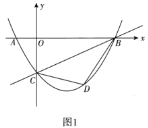
【题目】如图在平面直角坐标系中,一次函数![]() 的图象与
的图象与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,二次函数
,二次函数![]() 的图象经过
的图象经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴的负半轴交于点
轴的负半轴交于点![]() ,动点
,动点![]() 在直线
在直线![]() 下方的二次函数图象上.
下方的二次函数图象上.
(1)求二次函数的表达式;
(2)如图1,连接![]() ,
,![]() ,设
,设![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
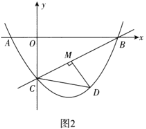
(3)如图2,过点![]() 作
作![]() 于点
于点![]() ,是否存在点
,是否存在点![]() ,使得
,使得![]() 中的某个角恰好等于
中的某个角恰好等于![]() 的2倍?若存在,直接写出点
的2倍?若存在,直接写出点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
【答案】1)![]() ;(2)S最大值为4;(3)存在,点D的横坐标为2或
;(2)S最大值为4;(3)存在,点D的横坐标为2或![]()
【解析】
(1)根据题意得到B、C两点的坐标,设抛物线的解析式为![]() ,将点C的坐标代入求得m的值即可;
,将点C的坐标代入求得m的值即可;
(2)过点D作DF⊥x轴,交BC与点F,设![]() ,则
,则![]() ,然后列出S与x的关系式,最后利用配方法求得其最大值即可;
,然后列出S与x的关系式,最后利用配方法求得其最大值即可;
(3)根据勾股定理的逆定理得到△ABC是以∠ACB为直角的直角三角形,取AB的中点E,EA=EC=EB=![]() ,过D作Y轴的垂线,垂足为R,交AC的延线于G,设
,过D作Y轴的垂线,垂足为R,交AC的延线于G,设![]() ,则DR=x,
,则DR=x,![]() ,最后,分为∠DCM=2∠BAC和∠MDC=2∠BAC两种情况列方程求解即可.
,最后,分为∠DCM=2∠BAC和∠MDC=2∠BAC两种情况列方程求解即可.
:(1)把x=0代入![]() 得y=-2,
得y=-2,
∴C(0,-2).
把y=0代![]() 得x=4,
得x=4,
∴B(4,0),
设抛物线的解析式为![]() ,将C(0,-2)代入得:2m=-2,解得:m=-1,∴A(-1,0).
,将C(0,-2)代入得:2m=-2,解得:m=-1,∴A(-1,0).
∴抛物线的解析式![]() ,即
,即![]() ;
;
(2)如图所示:过点D作DF⊥x轴,交BC与点F.
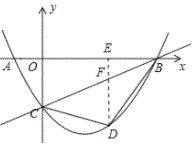
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴当x=2时,S有最大值,最大值为4.
(3)如图所示:过点D作DR⊥y垂足为R,DR交BC与点G.
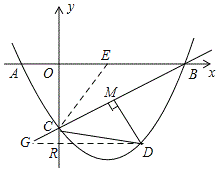
∵A(-1,0),B(4,0),C(0,-2),
∴![]() ,AB=5,
,AB=5,
∴AC2+BC2=AB2,
∴△ABC为直角三角形.
取AB的中点E,连接CE,则CE=BE,
∴∠OEC=2∠ABC.
∴![]() ,
,
当∠MCD=2∠ABC时,则tan∠CDR=tan∠ABC= ![]() ,
,
设![]() ,则DR=x,
,则DR=x,![]() ,
,
∴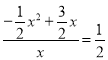 ,解得:x=0(舍去)或x=2.
,解得:x=0(舍去)或x=2.
∴点D的横坐标为2.
当∠CDM=2∠ABC时,设MD=3k,CM=4k,CD=5k.
∵tan∠MGD= ![]() ,
,
∴GM=6k,![]() ,
,
∴GC=MG-CM=2k,
∴![]() ,
,
∴![]() ,
,
∴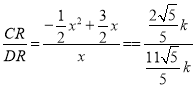 ,整理得:
,整理得:![]() ,
,
解得:x=0(舍去)或x=![]() .
.
∴点D的横坐标为![]() ,
,
综上所述,当点D的横坐标为2或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某次数学竞赛中有5道选择题,每题1分,每道题在![]() 、
、![]() 、
、![]() 三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
三个选项中,只有一个是正确的.下表是甲、乙、丙、丁四位同学每道题填涂的答案和这5道题的得分:
第一题 | 第二题 | 第三题 | 第四题 | 第五题 | 得分 | |
甲 |
|
|
|
|
| 4 |
乙 |
|
|
|
|
| 3 |
丙 |
|
|
|
|
| 2 |
丁 |
|
|
|
|
|
(1)则甲同学错的是第 题;
(2)丁同学的得分是 ;
(3)如果有一个同学得了1分,他的答案可能是 (写出一种即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
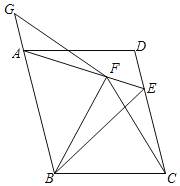
【题目】在平行四边形ABCD中,以AB为边作等边△ABE,点E在CD上,以BC为边作等边△BCF,点F在AE上,点G在BA延长线上且FG=FB.
(1)若CD=6,AF=3,求△ABF的面积;
(2)求证:BE=AG+CE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,已知格点四边形ABCD(顶点是网格线的交点)和格点O.

(1)将四边形ABCD先向左平移4个单位长度,再向下平移6个单位长度,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1,(点A,B,C,D的对应点分别为点A1,B1,C1,D1);
(2)将四边形ABCD绕点O逆时针旋转90°,得到四边形A2B2C2D2,画出旋转后的四边形A2B2C2D2(点A、B,C,D的对应点分别为点A2,B2,C2,D2);
(3)填空:点C2到A1D1的距离为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c交x轴于A(﹣1,0),B(3,0),交y轴的负半轴于C,顶点为D.下列结论:①2a+b=0;②2c<3b;③当m≠1时,a+b<am2+bm;④当△ABD是等腰直角三角形时,则a=![]() ;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.
;⑤当△ABC是等腰三角形时,a的值有3个.其中正确的有( )个.

A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“食品安全”受到全社会的广泛关注,育才中学对部分学生就食品安全知识的了解程度,采用随机抽样调查的方式,并根据收集到的信息进行统计,绘制了下面的两幅尚不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
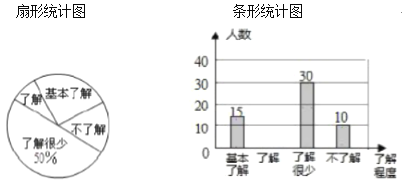
(1)接受问卷调查的学生共有________人,扇形统计图中“基本了解”部分所对应扇形的圆心角为_________![]() ;
;
(2)请补全条形统计图;
(3)若对食品安全知识达到“了解”程度的学生中,男、女生的比例恰为![]() ,现从中随机抽取
,现从中随机抽取![]() 人参加食品安全知识竞赛,则恰好抽到
人参加食品安全知识竞赛,则恰好抽到![]() 个男生和
个男生和![]() 个女生的概率________.
个女生的概率________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A点的坐标为(﹣1,5),B点的坐标为(3,3),C点的坐标为(5,3),D点的坐 标为(3,﹣1),小明发现:线段AB与线段CD存在一种特殊关系,即其中一条线段绕着某点旋转一个角度可以得到另一条线段,你认为这个旋转中心的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了方便学生在上下学期间安全过马路,南岸区政府决定在南开(融侨)中学校门口修建人行天桥(如图1),其平面图如图2所示,初三(8)班的学生小刘想利用所学知识测量天桥顶棚距地面的高度.天桥入口A点有一台阶AB=2m,其坡角为30°,在AB上方有两段平层BC=DE=1.5m,且BC,DE与地面平行,BC,DE上方又紧接台阶CD,EF,其长度相等且坡度均为i=4:3,顶棚距天桥距离FG=2m,且小刘从入口A点测得顶棚顶端G的仰角为37°,请根据以上数据,帮小刘计算出顶端G点距地面高度为( )m.(结果保留一位小数,参考数据:![]() ≈1.73,sin37°≈
≈1.73,sin37°≈![]() ,cos37°≈
,cos37°≈![]() ,tan37°≈
,tan37°≈![]() )
)
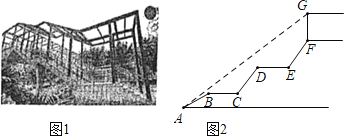
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com