
分析 仿照上述计算过程将原式变形,化简即可得到结果;原式括号中分母有理化后,利用平方差公式计算即可得到结果.
解答 解:$\frac{1}{\sqrt{11}+\sqrt{10}}$=$\frac{\sqrt{11}-\sqrt{10}}{(\sqrt{11}+\sqrt{10})(\sqrt{11}-\sqrt{10})}$=$\sqrt{11}$-$\sqrt{10}$,$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$,
原式=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2016}$-$\sqrt{2015}$)($\sqrt{2016}$+1)=($\sqrt{2016}$-1)($\sqrt{2016}$+1)=2016-1=2015,
故答案为:$\sqrt{11}$-$\sqrt{10}$;$\sqrt{n+1}$-$\sqrt{n}$;2015
点评 此题考查了分母有理化,二次根式有理化主要利用了平方差公式,所以一般二次根式的有理化因式是符合平方差公式的特点的式子.即一项符号和绝对值相同,另一项符号相反绝对值相同.


科目:初中数学 来源: 题型:解答题
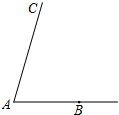 如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹)
如图,已知∠CAB,用直尺和圆规作∠ABD,使∠ABD=$\frac{1}{2}$∠A,射线BD与射线AC相交于点D.(不写画法,保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )
如图,是正方体包装盒的平面展开图,如果在其中的三个正方形A、B、C内分别填上适当的数,使得将这个平面展开图折成正方体后,相对面上的两数字互为相反数,则填在A、B、C内的三个数字依次为( )| A. | 0,1,-2 | B. | 1,0,-2 | C. | -2,0,1 | D. | 0,-2,1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com